题目内容
【题目】如图1和2,在20×20的等距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网的底部重合时,继续同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动.设运动时间为x秒,△QAC的面积为y.
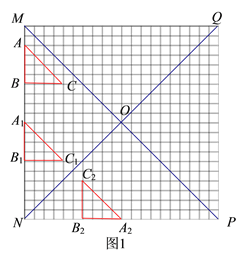
(1)如图1,当Rt△ABC向下平移到Rt△A1B1C1的位置时,请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形;
(2)如图2,在Rt△ABC向下平移的过程中,请你求出y与x的函数关系式,并说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?
(3)在Rt△ABC向右平移的过程中,请你说明当x取何值时,y取得最大值和最小值?最大值和最值分别是多少?为什么?(说明:在(3)中,将视你解答方法的创新程度,给予1~4分的加分)

【答案】(1)详见解析;(2)y=2x+40(0≤x≤16),当x=0时, y最小=40,当x=16时,y最大=72;(3)当x=32时, y最小=40;当x=16时, y最大=72.
【解析】试题分析:
(1)如图1,分别作出点A1、B1、C1关于直线QN的对称点A2、B2、C2,在顺次连接这三点即可得到所求三角形;
(2)如图2,当△ABC以每秒1个单位长的速度向下平移x秒时,则有:MA=x,MB=x+4,MQ=20,由题意可得:y= S梯形QMBC﹣S△AMQ﹣S△ABC,由此就可得到y与x之间的函数关系式,结合x的取值范围是![]() 即可求得y的最大值和最小值;
即可求得y的最大值和最小值;
(3)如图2,可用如下两种方法解答本问:
方法一:当△ABC继续以每秒1个单位长的速度向右平移时,此时16≤x≤32,PB=20﹣(x﹣16)=36﹣x,PC=PB﹣4=32﹣x,由y=S梯形BAQP﹣S△CPQ﹣S△ABC即可列出y与x之间的函数关系式,结合x的取值范围即可求得y的最大值和最小值;
方法二:在△ABC自左向右平移的过程中,△QAC在每一时刻的位置都对应着(2)中△QAC某一时刻的位置,使得这样的两个三角形关于直线QN成轴对称.因此,根据轴对称的性质,只需考查△ABC在自上向下平移过程中△QAC面积的变化情况,便可以知道△ABC在自左向右平移过程中△QAC面积的变化情况.
试题解析:
(1)如图1,△A2B2C2是△A1B1C1关于直线QN成轴对称的图形
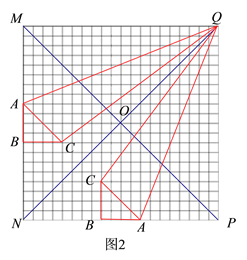
(2)当△ABC以每秒1个单位长的速度向下平移x秒时(如图2),
则有:MA=x,MB=x+4,MQ=20,
y=S梯形QMBC﹣S△AMQ﹣S△ABC
=![]() (4+20)(x+4)﹣
(4+20)(x+4)﹣![]() ×20x﹣
×20x﹣![]() ×4×4
×4×4
=2x+40(0≤x≤16).
由一次函数的性质可知:
当x=0时,y取得最小值,且y最小=40,
当x=16时,y取得最大值,且y最大=2×16+40=72;
(3)解法一:
当△ABC继续以每秒1个单位长的速度向右平移时,
此时16≤x≤32,PB=20﹣(x﹣16)=36﹣x,PC=PB﹣4=32﹣x,
∴y=S梯形BAQP﹣S△CPQ﹣S△ABC=![]() (4+20)(36﹣x)﹣
(4+20)(36﹣x)﹣![]() ×20×(32﹣x)﹣
×20×(32﹣x)﹣![]() ×4×4
×4×4
=﹣2x+104(16≤x≤32).
由一次函数的性质可知:
当x=32时,y取得最小值,且y最小=﹣2×32+104=40;
当x=16时,y取得最大值,且y最大=﹣2×16+104=72.
解法二:
在△ABC自左向右平移的过程中,
△QAC在每一时刻的位置都对应着(2)中△QAC某一时刻的位置,
使得这样的两个三角形关于直线QN成轴对称.
因此,根据轴对称的性质,
只需考查△ABC在自上至下平移过程中△QAC面积的变化情况,
便可以知道△ABC在自左向右平移过程中△QAC面积的变化情况.
当x=16时,y取得最大值,且y最大=72,
当x=32时,y取得最小值,且y最小=40.

【题目】将一副三角板中的两个直角顶点![]() 叠放在一起(如图①),其中
叠放在一起(如图①),其中![]() ,
,![]() ,
,![]() .
.

(1)猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)若按住三角板![]() 不动,绕顶点
不动,绕顶点![]() 转动三角
转动三角![]() ,试探究
,试探究![]() 等于多少度时
等于多少度时![]() ,并简要说明理由.
,并简要说明理由.
【题目】抛物线![]() 上部分点坐标如表所示,下列说法错误的是( )
上部分点坐标如表所示,下列说法错误的是( )
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -6 | 0 | 4 | 6 | 6 | … |
A. 抛物线与y轴的交点为(0,6) B. 抛物线的对称轴是在y轴的右侧;
C. 抛物线一定经过点(3,0) D. 在对称轴左侧,y随x增大而减小.
【题目】某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
甲 | 95 | 82 | 88 | 81 | 93 | 79 | 84 | 78 |
乙 | 83 | 92 | 80 | 95 | 90 | 80 | 85 | 75 |
(1)请你计算这两组数据的平均数、中位数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.


