ÌâÄṡÄÚÈÝ
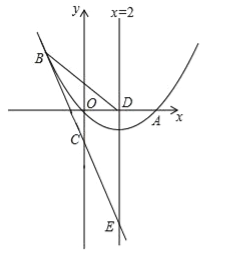
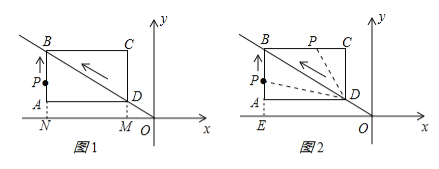
ḂẅÌâÄṡḂṡÈçÍỳ1£ỲẅØŴÎABCDṁÄÁẄÌõḟßÔÚṪøḟêÖáÉÏ£ỲṁãDÓëṪøḟêÔṁãOÖØẃÏ£ỲÇÒAD=8£ỲAB=6£®ÈçÍỳ2£ỲẅØŴÎABCDÑØOBṖẄÏòÒÔÃṡÃë1ẁöṁċÎṠġĊ¶ÈṁÄËÙ¶ÈÔ˶Ÿ£ỲÍỲÊḟṁãPṀÓAṁãġöṖḃÒĠÒÔÃṡÃë1ẁöṁċÎṠġĊ¶ÈṁÄËÙ¶ÈÑØẅØŴÎABCDṁÄḟßABẅṗýṁãBÏòṁãCÔ˶Ÿ£ỲṁḟṁãPṁẄṀïṁãCÊḟ£ỲẅØŴÎABCDẃÍṁãPÍỲÊḟÍ£ÖṗÔ˶Ÿ£ỲÉèṁãPṁÄÔ˶ŸÊḟỳäÎẂtÃ룮

£Ẁ1£©ṁḟt=5Êḟ£ỲÇëÖḟẄÓŴṀġöṁãDḂḃṁãPṁÄṪøḟê£Ṡ
£Ẁ2£©ṁḟṁãPÔÚÏ߶ÎABṠòÏ߶ÎBCÉÏÔ˶ŸÊḟ£ỲÇóġöḂṫPBDṁÄÃæṠýSṗØÓÚtṁÄẃŸÊýṗØÏṁÊẄ£ỲĠḃŴṀġöÏàÓḊtṁÄÈḂÖṁṖ¶Î§£Ṡ
£Ẁ3£©ṁãPÔÚÏ߶ÎABṠòÏ߶ÎBCÉÏÔ˶ŸÊḟ£ỲṪṫPEḂÍxÖá£ỲṀṗṪãÎẂṁãE£ỲṁḟḂṫPEOÓëḂṫBCDÏàËÆÊḟ£ỲÇóġöÏàÓḊṁÄtÖṁ£®
ḂẅṀŵḞẁḂṡ£Ẁ1£©D£Ẁ©4£Ỳ3£©£ỲP£Ẁ©12£Ỳ8£©£Ṡ£Ẁ2£©![]() £Ṡ£Ẁ3£©6£®
£Ṡ£Ẁ3£©6£®
ḂẅẄâÎöḂṡ
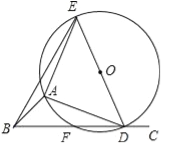
ÊÔÌâṖÖÎö£ẃ£Ẁ1£©ÑÓġĊCDẄṠxÖáÓÚM£ỲÑÓġĊBAẄṠxÖáÓÚN£ỲÔòCMḂÍxÖá£ỲBNḂÍxÖá£ỲADḂÎxÖá£ỲBNḂÎDM£ỲÓÉẅØŴÎṁÄŴÔÖÊṁÃġöẃÍṗṀṗɶẀÀíÇóġöBD£ỲBO=15£ỲÓÉÆẄŴŴÏßṁÃġöḂṫABDḂṪḂṫNBO£ỲṁÃġöḟÈÀýÊẄ![]() £ỲÇóġöBNḂḃNO£ỲṁÃġöOMḂḃDNḂḃPN£ỲỳṀṡÉṁÃġöṁãDḂḃPṁÄṪøḟê£Ṡ
£ỲÇóġöBNḂḃNO£ỲṁÃġöOMḂḃDNḂḃPN£ỲỳṀṡÉṁÃġöṁãDḂḃPṁÄṪøḟê£Ṡ
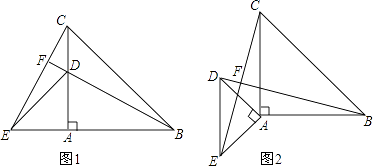
£Ẁ2£©ṁḟṁãPÔÚḟßABÉÏÊḟ£ỲBP=6©t£ỲÓÉÈýẄÇŴÎṁÄÃæṠýṗḋÊẄṁÃġöS=![]() BPAD£ṠḃÚṁḟṁãPÔÚḟßBCÉÏÊḟ£ỲBP=t©6£ỲÍỲÀíṁÃġöS=
BPAD£ṠḃÚṁḟṁãPÔÚḟßBCÉÏÊḟ£ỲBP=t©6£ỲÍỲÀíṁÃġöS=![]() BPAB£ṠỳṀṡÉṁÃġöẄáṗû£Ṡ
BPAB£ṠỳṀṡÉṁÃġöẄáṗû£Ṡ
£Ẁ3£©ÉèṁãD£Ẁ![]() £Ỳ
£Ỳ![]() £©£ṠṖÖÁẄÖÖÇéṡö£ẃḃÙṁḟṁãPÔÚḟßABÉÏÊḟ£ỲP£Ẁ
£©£ṠṖÖÁẄÖÖÇéṡö£ẃḃÙṁḟṁãPÔÚḟßABÉÏÊḟ£ỲP£Ẁ![]() £Ỳ
£Ỳ![]() £©£ỲÓÉ
£©£ỲÓÉ![]() ẃÍ
ẃÍ![]() Êḟ£ṠṖÖḟŵÇóġötṁÄÖṁ£Ṡ
Êḟ£ṠṖÖḟŵÇóġötṁÄÖṁ£Ṡ
ḃÚṁḟṁãPÔÚḟßBCÉÏÊḟ£ỲP£Ẁ![]() £Ỳ
£Ỳ![]() £©£ṠÓÉ
£©£ṠÓÉ![]() ẃÍ
ẃÍ![]() Êḟ£ỲṖÖḟŵÇóġötṁÄÖṁỳṀṡÉ£®
Êḟ£ỲṖÖḟŵÇóġötṁÄÖṁỳṀṡÉ£®
ÊÔÌâẄâÎö£ẃ£Ẁ1£©ÑÓġĊCDẄṠxÖáÓÚM£ỲÑÓġĊBAẄṠxÖáÓÚN£ỲÈçÍỳ1ËùÊẅ£ẃÔòCMḂÍxÖá£ỲBNḂÍxÖá£ỲADḂÎxÖá£ỲBNḂÎDM£ỲḂßËÄḟßŴÎABCDÊÇẅØŴΣỲḂàḂÏBAD=90Ḃã£ỲCD=AB=6£ỲBC=AD=8£ỲḂàBD=![]() =10£Ỳṁḟt=5Êḟ£ỲOD=5£ỲḂàBO=15£ỲḂßADḂÎNO£ỲḂàḂṫABDḂṪḂṫNBO£ỲḂà
=10£Ỳṁḟt=5Êḟ£ỲOD=5£ỲḂàBO=15£ỲḂßADḂÎNO£ỲḂàḂṫABDḂṪḂṫNBO£ỲḂà![]() £ỲỳṀ
£ỲỳṀ![]() £ỲḂàBN=9£ỲNO=12£ỲḂàOM=12©8=4£ỲDM=9©6=3£ỲPN=9©1=8£ỲḂàD£Ẁ©4£Ỳ3£©£ỲP£Ẁ©12£Ỳ8£©£Ṡ
£ỲḂàBN=9£ỲNO=12£ỲḂàOM=12©8=4£ỲDM=9©6=3£ỲPN=9©1=8£ỲḂàD£Ẁ©4£Ỳ3£©£ỲP£Ẁ©12£Ỳ8£©£Ṡ
£Ẁ2£©ÈçÍỳ2ËùÊẅ£ẃṁḟṁãPÔÚḟßABÉÏÊḟ£ỲBP=6©t£ỲḂàS=![]() BPAD=
BPAD=![]() £Ẁ6©t£©ḂÁ8=©4t+24£Ṡ
£Ẁ6©t£©ḂÁ8=©4t+24£Ṡ
ḃÚṁḟṁãPÔÚḟßBCÉÏÊḟ£ỲBP=t©6£ỲḂàS=![]() BPAB=
BPAB=![]() £Ẁt©6£©ḂÁ6=3t©18£Ṡ
£Ẁt©6£©ḂÁ6=3t©18£Ṡ
ṪÛÉÏËùÊö£ẃ![]() £Ṡ
£Ṡ
£Ẁ3£©Éèṁã D£Ẁ![]() £Ỳ
£Ỳ![]() £©£Ṡ
£©£Ṡ
ḃÙṁḟṁãPÔÚḟßABÉÏÊḟ£ỲP£Ẁ![]() £Ỳ
£Ỳ![]() £©£ỲÈô
£©£ỲÈô![]() Êḟ£Ỳ
Êḟ£Ỳ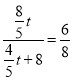 £ỲẄâṁãẃt=6£Ṡ
£ỲẄâṁãẃt=6£Ṡ
Èô![]() Êḟ£Ỳ
Êḟ£Ỳ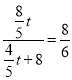 £ỲẄâṁãẃt=20£ẀĠṠẃÏÌâÒâ£ỲÉáÈċ£©£Ṡ
£ỲẄâṁãẃt=20£ẀĠṠẃÏÌâÒâ£ỲÉáÈċ£©£Ṡ
ḃÚṁḟṁãPÔÚḟßBCÉÏÊḟ£ỲP£Ẁ![]() £Ỳ
£Ỳ![]() £©£ỲÈô
£©£ỲÈô![]() Êḟ£Ỳ
Êḟ£Ỳ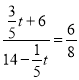 £ỲẄâṁãẃt=6£Ṡ
£ỲẄâṁãẃt=6£Ṡ
Èô![]() Êḟ£Ỳ
Êḟ£Ỳ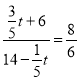 £ỲẄâṁãẃ
£ỲẄâṁãẃ![]() £ẀĠṠẃÏÌâÒâ£ỲÉáÈċ£©£Ṡ
£ẀĠṠẃÏÌâÒâ£ỲÉáÈċ£©£Ṡ
ṪÛÉÏËùÊö£ẃṁḟt=6Êḟ£ỲḂṫPEOÓëḂṫBCDÏàËÆ£®

ḂẅÌâÄṡḂṡÄġḞà50ÃûѧÉúṁÄÒṠṀÎḞĠÈḋÖẂʶẅẃÈüġÉỳẀ£ẀÂúṖÖÎẂ10ṖÖ£©ṖÖĠỳÈçḟíËùÊẅ£ẃ
ġÉỳẀ£ẀṖÖ£© | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
ÈËÊý£ẀÈË£© | 0 | 0 | 0 | 1 | 0 | 1 | 3 | 5 | 6 | 19 | 15 |
ÕâṀÎḞĠÈḋÖẂʶẅẃÈüġÉỳẀṁÄÖÚÊýÊÇ£Ẁ £©
A. 5ṖÖ B. 6ṖÖ C. 9ṖÖ D. 10ṖÖ