��Ŀ����
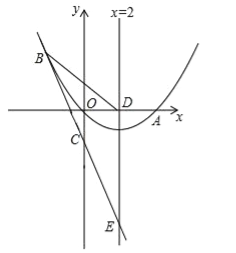
����Ŀ����ͼ����֪�����߾���ԭ��o��x����һ��A��4��0���������߶���ΪE�����ĶԳ�����x�ύ�ڵ�D��ֱ��y=��2x��1������������һ��B����2��m������y�ύ�ڵ�C���������ߵĶԳ��ύ�ڵ�F��
��1����m��ֵ���������߶�Ӧ�Ľ���ʽ��
��2��P��x��y�����������ϵ�һ�㣬��S��ADP=S��ADC��������з��������ĵ�P�����ꣻ
��3����Q��ƽ��������һ�㣬��M�ӵ�F�������ضԳ���������ÿ��1����λ���ȵ��ٶ������˶������M���˶�ʱ��Ϊt�룬�Ƿ���ʹ��Q��A��E��M�ĵ�Ϊ������ı��������Σ����ܣ���ֱ��д����M���˶�ʱ��t��ֵ�������ܣ���˵�����ɣ�
���𰸡���1��3��![]() ����2��P1��
����2��P1��![]() ��1����P2��
��1����P2��![]() ��1����P3��2����1������3��t1=
��1����P3��2����1������3��t1=![]() ��t2=6��t3=
��t2=6��t3=![]() ��t4=6.5��
��t4=6.5��
��������
�����������1�����������B�������m��ֵ��Ȼ�����ô���ϵ������������ߵĽ���ʽ��
��2����ADP����ADC�й�ͬ�ĵױ�AD����Ϊ�����ȣ�����AD���ϵĸ���ȣ���Ϊ1���Ӷ��õ���P��������Ϊ1�������������ߵĽ���ʽ�����P�������ꣻ
��3������ͼ��ʾ���ڵ�M���˶������У����γ����ĸ����Σ�ע�ⲻҪ©�⣮���ÿһ�����Σ��ֱ���м��㣬����߶�MF�ij��ȣ��Ӷ��õ��˶�ʱ��t��ֵ��
�����������1������B����2��m����ֱ��y=��2x��1������m=��2������2����1=4��1=3�����ԣ���B����2��3�������������߾���ԭ��O�����������ߵĽ���ʽΪy=ax2+bx������B����2��3����A��4��0�����������ϣ���![]() ����ã�
����ã� ���������ߵĽ���ʽΪ
���������ߵĽ���ʽΪ![]() ��
��
��2����P��x��y�����������ϵ�һ�㣬��P��x��![]() ������S��ADP=S��ADC����S��ADC=
������S��ADP=S��ADC����S��ADC=![]() ADOC��S��ADP=
ADOC��S��ADP=![]() AD|y|��������C��ֱ��y=��2x��1��y�ύ�㣬��C��0����1������OC=1����|
AD|y|��������C��ֱ��y=��2x��1��y�ύ�㣬��C��0����1������OC=1����|![]() |=1����
|=1����![]() =1��
=1��![]() =��1����ã�x1=
=��1����ã�x1=![]() ��x2=
��x2=![]() ��x3=x4=2������P������Ϊ P1��
��x3=x4=2������P������Ϊ P1��![]() ��1����P2��
��1����P2��![]() ��1����P3��2����1����
��1����P3��2����1����
��3�����ۣ����ڣ���ͼ2
�������ߵĽ���ʽΪ![]() ��������E��2����1�����Գ���Ϊx=2��
��������E��2����1�����Գ���Ϊx=2��
��F��ֱ��y=��2x��1��Գ���x=2�Ľ��㣬��F��2����5����DF=5��
����A��4��0������AE=![]() ��
��
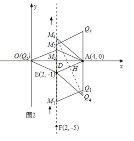
����ͼ��ʾ���ڵ�M���˶������У����γ����ĸ����Σ�
������AEM/span>1Q1��
����ʱEM1=AE=![]() ����M1F=DF��DE��DM1=
����M1F=DF��DE��DM1=![]() ����t1=
����t1=![]() ��
��
������AEOM2��
����ʱDM2=DE=1����M2F=DF+DM2=6����t2=6��
������AEM3Q3��
����ʱEM3=AE=![]() ����DM3=EM3��DE=
����DM3=EM3��DE=![]() ��1����M3F=DM3+DF=��
��1����M3F=DM3+DF=��![]() ��1��+5=
��1��+5=![]() ����t3=
����t3=![]() ��
��
������AM4EQ4��
��ʱAEΪ���εĶԽ��ߣ���Խ���AE��M4Q4���ڵ�H����AE��M4Q4������֪��AED�ס�M4EH����![]() ����
���� ����M4E=2.5����DM4=M4E��DE=2.5��1=1.5����M4F=DM4+DF=1.5+5=6.5����t4=6.5��
����M4E=2.5����DM4=M4E��DE=2.5��1=1.5����M4F=DM4+DF=1.5+5=6.5����t4=6.5��
�������������ڵ�M����Q��ʹ����Q��A��E��M�ĵ�Ϊ������ı��������Σ�ʱ��t��ֵΪ��t1=![]() ��t2=6��t3=
��t2=6��t3=![]() ��t4=6.5��
��t4=6.5��


 ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�