题目内容
【题目】若顺次连结四边形各边中点所得的四边形是矩形,则原四边形( )
A. 一定是矩形 B. 一定是菱形 C. 对角线一定相等 D. 对角线一定互相垂直
【答案】D
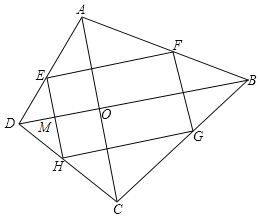
【解析】分析:根据题意画出相应的图形,如图所示,由四边形EFGH为矩形,根据矩形的四个角为直角得到∠FEH=90°,又EF为三角形ABD的中位线,根据中位线定理得到EF与DB平行,根据两直线平行,同旁内角互补得到∠EMO=90°,同理根据三角形中位线定理得到EH与AC平行,再根据两直线平行,同旁内角互补得到∠AOD=90°,根据垂直定义得到AC与BD垂直.
详解:
∵四边形EFGH是矩形,
∴∠FEH=90°,
又∵点E、F、分别是AD、AB、各边的中点,
∴EF是三角形ABD的中位线,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵点E、H分别是AD、CD各边的中点,
∴EH是三角形ACD的中位线,
∴EH∥AC,
∴∠OMH=∠COB=90°,
即AC⊥BD.
故选:D.

练习册系列答案
相关题目
【题目】将从1开始的连续自然数按图规律排列:规定位于第m行,第n列的自然数10记为(3,2),自然数15记为(4,2)…
列 行 | 第1列 | 第2列 | 第3列 | 第4列 |
第1行 | 1 | 2 | 3 | 4 |
第2行 | 8 | 7 | 6 | 5 |
第3行 | 9 | 10 | 11 | 12 |
第4行 | 16 | 15 | 14 | 13 |
… | … | … | … | … |
第n行 | … | … | … | … |
按此规律,回答下列问题:
(1)记为(6,3)表示的自然数是__________________.
(2)自然数2018记为_________________.
(3)用一个正方形方框在第span>3列和第4列中任意框四个数,这四个数的和能为2018吗?如果能,求出框出的四个数中最小的数;如果不能,请写出理由。