Question

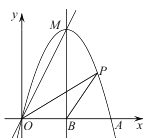
【题目】如图，直线y＝2x﹣1分别交x，y轴于点A，B，点C在x轴的正半轴，且∠ABC＝45°，则直线BC的函数表达式是_____．

Answer 1

【答案】y＝x﹣1

【解析】

过A作AF⊥AB交BC于F，过F作FE⊥x轴于E，判定△ABO≌△FAE（AAS），即可得出OB， OA得到点F坐标，从而得到直线BC的函数表达式．

解：∵一次函数y＝2x﹣1的图象分别交x、y轴于点A、B，

∴令x＝0，得y＝﹣1；令y＝0，则x＝，

∴A（，0），B（0，﹣1），

∴OA＝，OB＝1，

如图，过A作AF⊥AB交BC于F，过F作FE⊥x轴于E，

∵∠ABC＝45°，

∴△ABF是等腰直角三角形，

∴AB＝AF，

∵∠OAB+∠ABO＝∠OAB+∠EAF＝90°，

∴∠ABO＝∠EAF，

∴△ABO≌△FAE（AAS），

∴AE＝OB＝1，EF＝OA＝，

∴F（，﹣），

设直线BC的函数表达式为：y＝kx+b，则

，

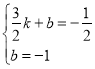解得，

∴直线BC的函数表达式为：y＝x﹣1，

故答案为：y＝x﹣1．