题目内容
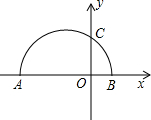 如图,已知两点A(-8,0),C(0,4),以AB为直径的半圆与y轴正半轴交于点C.
如图,已知两点A(-8,0),C(0,4),以AB为直径的半圆与y轴正半轴交于点C.(1)求过A、C两点的直线的解析式和经过A、B、C三点的抛物线的解析式;
(2)若点D是(1)中抛物线的顶点,求△ACD的面积.
分析:(1)可根据A、C的坐标用待定系数法求出直线AC的解析式.
连接AC,BC,在直角三角形ACB中,可用射影定理求出OB的长,即可得出B点的坐标.然后用待定系数法求出抛物线的解析式.
(2)由于△ACD的面积无法直接求出,因此可化为其他图形面积的和差来进行求解.
设抛物线的对称轴与直线BC交于E点,可先根据直线AC的解析式求出E点的坐标,然后分别计算出三角形ADE和CDE的面积,即可得出三角形ACD的面积.
连接AC,BC,在直角三角形ACB中,可用射影定理求出OB的长,即可得出B点的坐标.然后用待定系数法求出抛物线的解析式.
(2)由于△ACD的面积无法直接求出,因此可化为其他图形面积的和差来进行求解.
设抛物线的对称轴与直线BC交于E点,可先根据直线AC的解析式求出E点的坐标,然后分别计算出三角形ADE和CDE的面积,即可得出三角形ACD的面积.
解答: 解:(1)连接AC、BC.则有∠ACB=90°,根据射影定理有:
解:(1)连接AC、BC.则有∠ACB=90°,根据射影定理有:
OC2=OA•OB,
∴OB=OC2÷OA=16÷8=2
∴B(2,0)
设直线AC的解析式为y=kx+4,已知直线AC过A(-8,0),则有
-8k+4=0,k=
.
∴直线AC的解析式为:y=
x+4
设抛物线的解析式为y=a(x+8)(x-2),
已知抛物线过C(0,4),因此:
a(0+8)(0-2)=4,a=-
∴抛物线的解析式为y=-
(x+8)(x-2)=-
(x+3)2+
.
(2)易知:D(-3,
)
设直线AE与抛物线对称轴交于E点,则有E(-3,
)
因此DE=
∴S△ACD=S△AED+S△CDE=
×
×5+
×
×3=15(平方单位).
 解:(1)连接AC、BC.则有∠ACB=90°,根据射影定理有:
解:(1)连接AC、BC.则有∠ACB=90°,根据射影定理有:OC2=OA•OB,
∴OB=OC2÷OA=16÷8=2
∴B(2,0)
设直线AC的解析式为y=kx+4,已知直线AC过A(-8,0),则有
-8k+4=0,k=
| 1 |
| 2 |
∴直线AC的解析式为:y=
| 1 |
| 2 |
设抛物线的解析式为y=a(x+8)(x-2),
已知抛物线过C(0,4),因此:
a(0+8)(0-2)=4,a=-
| 1 |
| 4 |
∴抛物线的解析式为y=-
| 1 |
| 4 |
| 1 |
| 4 |
| 25 |
| 4 |
(2)易知:D(-3,
| 25 |
| 4 |
设直线AE与抛物线对称轴交于E点,则有E(-3,
| 5 |
| 2 |
因此DE=
| 15 |
| 4 |
∴S△ACD=S△AED+S△CDE=
| 1 |
| 2 |
| 15 |
| 4 |
| 1 |
| 2 |
| 15 |
| 4 |
点评:本题考查了二次函数解析式的确定,图形面积的求法等知识点.

练习册系列答案
相关题目
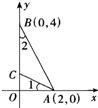 如图,已知两点A(2,0),B(0,4),且∠1=∠2,则点C的坐标是
如图,已知两点A(2,0),B(0,4),且∠1=∠2,则点C的坐标是 如图,已知两点A(2,0),B(0,4),且sin∠1=cos∠2,则点C的坐标为
如图,已知两点A(2,0),B(0,4),且sin∠1=cos∠2,则点C的坐标为 如图,已知两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3把线段AB缩小,则点A的对应点坐标是
如图,已知两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3把线段AB缩小,则点A的对应点坐标是 如图,已知两点P、Q在锐角∠AOB内,分别在OA、OB上求作点M、N,使PM+MN+NQ最短.
如图,已知两点P、Q在锐角∠AOB内,分别在OA、OB上求作点M、N,使PM+MN+NQ最短.