题目内容
 如图,已知两点A(2,0),B(0,4),且sin∠1=cos∠2,则点C的坐标为
如图,已知两点A(2,0),B(0,4),且sin∠1=cos∠2,则点C的坐标为(0,1)
(0,1)
.分析:根据已知条件,由勾股定理得到AB的长,从而求出cos∠2的值,即sin∠1的值,在Rt△OAC中,运用三角函数的知识求得AC,再由勾股定理得到OC的长,从而求解.
解答:解:∵A(2,0),B(0,4),
∴AB=
=2
,
∴sin∠1=cos∠2=
=
,
∴在Rt△OAC中,AC=
=
,
∴OC=1.
∴点C的坐标是(0,1).
故答案为:(0,1).
∴AB=
| 22+42 |
| 5 |
∴sin∠1=cos∠2=
| 4 | ||
2
|
2
| ||
| 5 |
∴在Rt△OAC中,AC=
| 2 | ||||
|
| 5 |
∴OC=1.
∴点C的坐标是(0,1).
故答案为:(0,1).
点评:本题考查了勾股定理,锐角三角函数的定义和坐标与图形性质.求点的坐标的问题可以转化为求线段的长度的问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
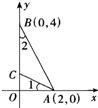 如图,已知两点A(2,0),B(0,4),且∠1=∠2,则点C的坐标是
如图,已知两点A(2,0),B(0,4),且∠1=∠2,则点C的坐标是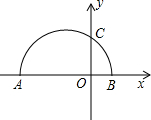 如图,已知两点A(-8,0),C(0,4),以AB为直径的半圆与y轴正半轴交于点C.
如图,已知两点A(-8,0),C(0,4),以AB为直径的半圆与y轴正半轴交于点C. 如图,已知两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3把线段AB缩小,则点A的对应点坐标是
如图,已知两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3把线段AB缩小,则点A的对应点坐标是 如图,已知两点P、Q在锐角∠AOB内,分别在OA、OB上求作点M、N,使PM+MN+NQ最短.
如图,已知两点P、Q在锐角∠AOB内,分别在OA、OB上求作点M、N,使PM+MN+NQ最短.