题目内容
【题目】已知函数y=![]() 为反比例函数.
为反比例函数.
(1)求k的值;
(2)它的图象在第 象限内,在各象限内,y随x增大而 ;(填变化情况)
(3)求出﹣2≤x≤﹣![]() 时,y的取值范围.
时,y的取值范围.
【答案】(1)k=﹣2;(2)二、四,增大;(3)2≤y≤8.
【解析】试题分析:(1)根据反比例函数的定义确定k的值即可;
(2)根据反比例函数的性质结合求得的k的符号描述其图象的位置及增减性即可;
(3)分别代入自变量的值结合其增减性即可确定函数值的取值范围.
试题解析:(1)由题意得:k2﹣5=﹣1,
解得:k=±2,
∵k﹣2≠0,
∴k=﹣2;
(2)∵k=﹣2<0,
∴反比例函数的图象在二、四象限,在各象限内,y随着x增大而增大;
故答案为:二、四,增大;
(3)∵反比例函数表达式为![]() ,
,
∴当x=﹣2时,y=2,当x=![]() 时,y=8,
时,y=8,
∴当-2≤x≤![]() 时,2≤y≤8.
时,2≤y≤8.

练习册系列答案
相关题目
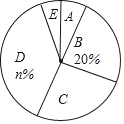
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.
类别 | A | B | C | D | E |
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 12 | 30 | m | 54 | 9 |
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %.
(2)被调查学生的总人数为 人,统计表中m的值为 ,统计图中n的值为 ;
(3)在统计图中,B类所对应扇形圆心角的度数为 ;
(4)该校共有1000名学生,根据调查结果,估计该校最喜爱A类节目的人数.