题目内容
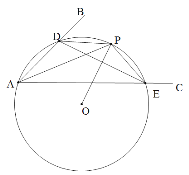
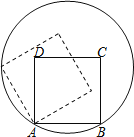
【题目】如图，已知正方形ABCD的顶点A、B在⊙O上，顶点C、D在⊙O内，将正方形ABCD绕点A逆时针旋转，使点D落在⊙O上，若正方形ABCD的边长和⊙O的半径均为6cm，则点D运动的路径长为（ ）
A.2πcmB.
cmC.πcmD.
cm
【答案】C
【解析】
设圆心为O，连接AO，BO，AC，AE，OF，易证三角形AOB是等边三角形，确定∠EAC=30°，再利用弧长公式计算即可．
设圆心为O，连接AO，BO，AC，AE，OF，
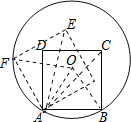
∵AB＝6，AO＝BO＝6，
∴AB＝AO＝BO，
∴三角形AOB是等边三角形，
∴∠AOB＝∠OAB＝60°
同理：△FAO是等边三角形，∠FAB＝2∠OAB＝120°，
∴∠EAC＝∠DAF=∠FAB-∠DAB=120°﹣90°＝30，
∵AD＝AB＝6，
∴点D运动的路径长为：
＝π．
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
