Question

【题目】在菱形ABCD中，∠BAD=60°

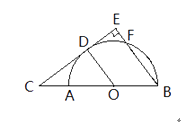
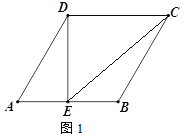
（1）如图1，点E为线段AB的中点，连接DE、CE，若AB=4，求线段EC的长；

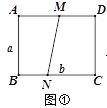
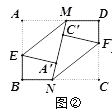
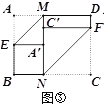
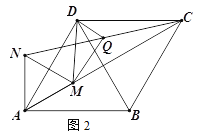
（2）如图2，M为线段AC上一点（不与A、C重合），以AM为边向上构造等边三角形AMN，连接NC、DM，Q为线段NC的中点，连接DQ、MQ，判断DM与DQ的数量关系，并证明你的结论.

Answer 1

【答案】（1）；（2）见解析；

【解析】（1）连接DB，利用菱形的性质、等边三角形的性质及勾股定理即可求解；

（2）延长MQ到H，使QH=MQ，连接DH、HC ，利用全等三角形的判定和性质、菱形的性质、勾股定理等即可求解.

（1）∵菱形ABCD，

∴AD=DC=AB，DC∥AB，

∴∠DEA=∠CDE，

连接DB，

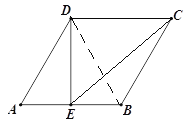
∵∠BAD=60°，

∴△ADB是等边三角形 ，

∵E为AB中点，

∴DE⊥AB，AE=，

∴∠DEA=90°，

∴∠CDE=90°，

在Rt△ADE中，AD=AB=4，AE==2，

∴DE= ，

在Rt△DCE中，DC=AB=4，

∴EC=；

（2）延长MQ到H，使QH=MQ，连接DH、HC ，

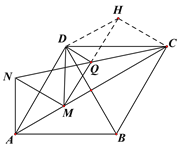
∵Q为NC中点，

∴NQ=CQ，

∵∠NQM=∠CQH，

∴△NQM≌△CQH（SAS），

∴NM=CH，∠MNQ=∠HCQ，

∴NM∥CH，

∴∠NMA=∠HCM，

∵有等边△AMN，

∴NM=AM，∠NMA=60°，

∴AM=CH，∠HCM=60°，

∵有菱形ABCD，AC为对角线，∠BAD=60°，

∴∠DAM=，

同理，∠DCA=30°，

∴∠HCD=30°，

∴△DAM≌△DCH（SAS），

∴DM=DH，∠ADM=∠CDH，

∴DQ⊥MH，∠MDQ=∠HDQ，∠MDH=∠ADC，

∴∠DQM=90°，

∵有菱形ABCD，∠BAD=60°，

∴∠ADC=120°，

∴∠MDH=120°，

∴∠MDQ=60°，

∴∠DMQ=30°，

∴DM=2DQ.