题目内容
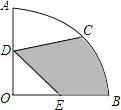
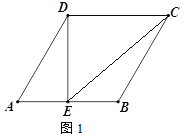
【题目】如图①,矩形纸片ABCD的边长分别为a、b(a<b),点M、N分别为边AD、BC上两点(点A、C除外),连接MN.
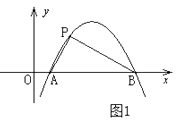
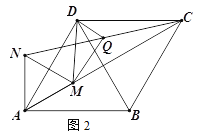
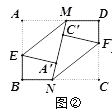
(1)如图②,分别沿ME、NF 将MN两侧纸片折叠,使点A、C分别落在MN上的A′、C′处,直接写出ME与FN的位置关系;
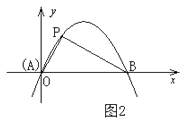
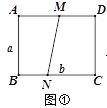
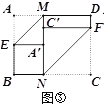
(2)如图③,当MN⊥BC 时,仍按(1)中的方式折叠,请求出四边形A′EBN与四边形C′FDM 的周长(用含a的代数式表示),并判断四边形A′EBN与四边形C′FDM周长之间的数量关系;
(3)如图④,若对角线BD与MN交于点O,分别沿BM、DN将MN两侧纸片折叠,折叠后,点A、C恰好都落在点O处,并且得到的四边形BNDM是菱形,请你探索a、b之间的数量关系.

【答案】(1)EM∥NF ;(2)![]() 的周长与
的周长与![]() 的周长相等;(3)
的周长相等;(3)![]()
【解析】(1)先根据翻折变换的性质得到∠EMN=![]() ∠AMN,∠FNC′=
∠AMN,∠FNC′=![]() ∠MNC,再由平行线的性质可得到∠AMN=∠MNC,由平行线的判定定理即可得到ME∥FN;
∠MNC,再由平行线的性质可得到∠AMN=∠MNC,由平行线的判定定理即可得到ME∥FN;
(2)由折叠得知:A′E=AE,根据四边形A′EBN是矩形,即可求出四边形A′EBN的即四边形C′FDM的周长;
(3)根据折叠的性质可知OD=CD=OB=a,在△BCD中利用勾股定理即可求出b的值.
(1)EM∥NF ;
(2)∵矩形ABCD,
∴∠A=90°=∠B,
∵△AEM沿EM折叠到△![]()
∴∠![]() ,AE=
,AE=![]()
∵MN⊥BC,
∴∠MNB=90°,
∴有矩形![]() ,
,
∴其周长为![]() ,
,
同理 四边形![]() 也为矩形,周长为,
也为矩形,周长为,
![]() ,
,
∴![]() 的周长与
的周长与![]() 的周长相等;
的周长相等;
(3)∵四边形BNDM是菱形,
∴BM=MD,BD⊥MN,BO=DO,MO=NO,∠MBO=∠NBO,
∵△ABM沿BM折叠到△OBM,
∴AB=OB,AM=MO,∠ABM=∠OBM,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠MBO=30°,
在Rt△MBO中,∠MOB=90°,
∴BM=2MO,
设MO=x,BM=2x,
BO=![]()
AD=AM+MD=BM+MO=3x
∴![]() ,即
,即![]() .
.