Question

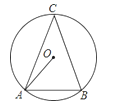
【题目】如图，⊙O是△ABC的外接圆，C是优弧AB上一点，设∠OAB=α，∠C=β．

（1）当β=36°时，求α的度数；

（2）猜想α与β之间的关系，并给予证明．

（3）若点C平分优弧AB，且BC2=3OA2 ，试求α的度数．

Answer 1

【答案】（1）β=54°；（2）α与β之间的关系是α+β=90°；证明见解析；（3）α=30°．

【解析】

（1）连接OB，根据同弧所对的圆周角是圆心角的一半和等腰三角形的性质解答即可；

（2）根据（1）的方法解答即可；

（3）过O作OE⊥AC于E，连接OC，证明AE=OA，得到△ABC为正三角形，得到答案．

（1）连接OB，

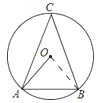
则OA=OB，

∴∠OAB=∠OBA，

∵∠C=36°，

∴∠AOB=72°，

∵∠OAB=（180°﹣∠AOB）=54°，

即β=54°；

（2）α与β之间的关系是α+β=90°；

证明：∵∠OBA=∠OAB=α，

∴∠AOB=180°﹣2α，

∵∠AOB=2∠β，

∴180°﹣2α=2∠β，

∴α+β=90°；

（3）∵点C平分优弧AB，

∴AC=BC，

又∵BC2=3OA2，

∴AC=BC=OA，

过O作OE⊥AC于E，连接OC，

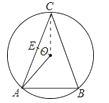
由垂径定理可知AE=OA，

∴∠AOE=60°，∠OAE=30°，

∴∠ABC=60°，

∴△ABC为正三角形，

则α=∠CAB﹣∠CAO=30°．