题目内容
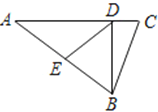
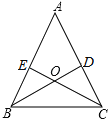
【题目】如图,△ABC的两条高BD、CE相交于点O 且OB=OC.则下列结论:
①△BEC≌△CDB;
②△ABC是等腰三角形;
③AE=AD;
④点O在∠BAC的平分线上,
其中正确的有_____.(填序号)
【答案】①②③④
【解析】
由三角形内角和定理可得∠ABC=∠ACB,可得AB=AC;由AAS可证△BEC≌△CDB;可得BE=CD,可得AD=AE;通过证明△AOB≌△AOC,可证点O在∠BAC的平分线上.即可求解.
解:∵OB=OC,
∴∠OBC=∠OCB,
∵锐角△ABC的两条高BD、CE相交于点O,
∴∠BEC=∠CDB=90°,
∵∠BEC+∠BCE+∠ABC=∠CDB+∠DBC+∠ACB=180°,
∴180°﹣∠BEC﹣∠BCE=180°﹣∠CDB﹣∠CBD,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形,故②符合题意;
∵∠OBC=∠OCB,∠BDC=∠BEC=90°,且BC=BC,
∴△BEC≌△CDB(AAS),故①符合题意,
∴BE=CD,且AB=AC,
∴AD=AE,故③符合题意;
连接AO并延长交BC于F,

在△AOB和△AOC中,

∴△AOB≌△AOC(SSS).
∴∠BAF=∠CAF,
∴点O在∠BAC的角平分线上,故④符合题意,
故正确的答案为:①②③④.

【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30
【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生,在这次义卖活动中,某班级售书情况如下表:
售价 |
|
|
|
|
数目 |
|
|
|
|
下列说法正确的是( )
A.该班级所售图书的总收入是![]() 元B.在该班级所传图书价格组成的一组数据中,中位数是
元B.在该班级所传图书价格组成的一组数据中,中位数是![]() 元
元
C.在该班级所售图书价格组成的一组数据中,众数是![]() 元D.在该班级所售图书价格组成的一组数据中,平均数是
元D.在该班级所售图书价格组成的一组数据中,平均数是![]() 元
元