Question

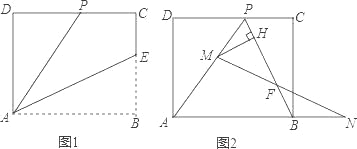
【题目】（探究）如图1，在等边△ABC中，AB＝4，点D、E分别为边BC、AB上的点，连结AD、DE，若∠ADE＝60°，BD＝3，求BE的长．

（拓展）如图2，在△ABD中，AB＝4，点E为边AB上的点，连结DE，若∠ADE＝∠ABD＝45°，若DB＝3，＝　 ．

Answer 1

【答案】【探究】BE＝；【拓展】

【解析】

探究：过点A作AF⊥BC于F，由等边三角形的性质得出BF=CF=BC=2，由勾股定理求出AF=，则DF=BD-BF=1，由勾股定理求出AD=，证得△ABD∽△ADE，得出，解得AE=，即可得出结果；

拓展：过点A作AF⊥BC于F，易证△ABF是等腰直角三角形，则AF=BF=AB=2，DF=DB-BF=，由勾股定理求出AD=，证得△ADE∽△ABD，得出，求出AE=，BD=AB-AE=，则即可得出结果．

探究：∵△ABC是等边三角形，

∴∠B=∠C=60°，AB=BC=4，

过点A作AF⊥BC于F，如图①所示：

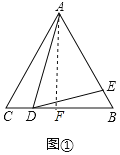
则BF=CF=BC=2，AF=，

∴DF=BD-BF=3-2=1，

∴AD=，

根据三角形的内角和定理得，∠ADB+∠BAD=120°，

∵∠ADE=60°，

∴∠BAD+∠AED=120°，

∴∠ADB=∠AED，

∵∠B=∠ADE=60°，

∴△ABD∽△ADE，

∴，

即：，

解得：AE=，

∴BE=AB-AE=4-=；

拓展：过点A作AF⊥BC于F，如图②所示：

∵∠ABD=45°，

∴△ABF是等腰直角三角形，

∴AF=BF=AB=2，

∴DF=DB-BF=3-2=，

∴AD=，

∵∠ADE=∠ABD=45°，∠A=∠A，

∴△ADE∽△ABD，

∴，

∴AE=，

∴BD=AB-AE=4-=，

∴．