题目内容
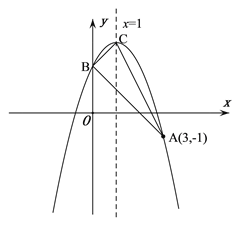
【题目】已知抛物线y＝ax2+bx+3过A(﹣3，0)，B(1，0)两点，交y轴于点C．
(1)求该抛物线的表达式．
(2)设P是该抛物线上的动点，当△PAB的面积等于△ABC的面积时，求P点的坐标．
【答案】(1)y＝﹣x2﹣2x+3；(2)P点坐标为(﹣1+
，﹣3)或(﹣1﹣，﹣3)．
【解析】
（1）把A与B坐标代入求出a与b的值，即可确定出表达式；
（2）先求出点C的坐标，从而确定△ABC的面积，再根据△PAB的面积等于△ABC的面积求出P的坐标即可．
解：(1)把A与B坐标代入得：
，
解得：
，
则该抛物线的表达式为y＝﹣x2﹣2x+3；
(2)由抛物线解析式得：C(0，3)，
∴△ABC面积为
×3×4＝6，
∴△PAB面积为6，即×|yP纵坐标|×4＝6，即yP纵坐标＝3或﹣3，
当yP纵坐标＝3时，可得3＝﹣x2﹣2x+3，
解得：x＝﹣2或x＝0(舍去)，
此时P坐标为(﹣2，3)；
当yP纵坐标＝﹣3时，可得﹣3＝﹣x2﹣2x+3，
解得：x＝﹣1±，
此时P坐标为(﹣1+，﹣3)或(﹣1﹣，﹣3)．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
