Question

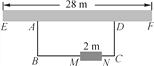
【题目】如图，利用一面墙(墙EF最长可利用28米)，围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示，不用砌墙)．现有砌60米长的墙的材料．

(1)当矩形的长BC为多少米时，矩形花园的面积为300平方米；

(2)能否围成480平方米的矩形花园，为什么？

Answer 1

【答案】(1) 当矩形的长BC为12米时，矩形花园的面积为300平方米．(2)不能围成480平方米的矩形花园．

【解析】试题分析：（1）利用设矩形花园的长BC为x米,用长表示宽，再列出面积的方程，解方程.

（2）由（1）的方程，令其等于480，解方程，求解与已知墙壁比较.

试题解析：

(1)设矩形花园的长BC为x米，则其宽为 (60－x＋2)米，依题意列方程，得 (60－x＋2)x＝300.

整理，得x2－62x＋600＝0.

解得x1＝12，x2＝50.

∵28＜50，

∴x2＝50不合题意，舍去．

∴x＝12.

答：当矩形的长BC为12米时，矩形花园的面积为300平方米．

(2)由题意得 (60－x＋2)x＝480，整理，得x2－62x＋960＝0.解得x1＝32，x2＝30.

∵28＜30＜32，

∴x1＝32，x2＝30均不合题意，舍去．

答：不能围成480平方米的矩形花园．