Question

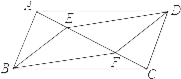
【题目】如图，E、F是ABCD对角线AC上两点，且AE＝CF．

（1）求证：四边形BFDE是平行四边形．

（2）如果把条件AE＝CF改为BE＝DF，试问四边形BFDE还是平行四边形吗？为什么？

Answer 1

【答案】（1）详见解析；（2）四边形BFDE不是平行四边形，理由详见解析.

【解析】

（1）根据对角线互相平分的四边形是平行四边形即可证明；

（2）四边形BFDE不是平行四边形.

（1）证明：连接BD，交AC于点O．

∵ABCD是平行四边形

∴OA＝OC OB＝OD（平行四边形的对角线互相平分）

又∵AE＝CF

∴OA﹣AE＝OC﹣CF，即OE＝OF

∴四边形BFDE是平行四边形（对角线互相平分的四边形是平行四边形）

（2）四边形BFDE不是平行四边形

因为把条件AE＝CF改为BE＝DF后，不能证明△BAE与△DCF全等．