Question

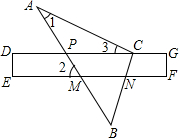如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，
（1）作出△APC的PC边上的高；
（2）若∠2=51°，求∠3；
（3）若直尺上点P处刻度为2，点C处为8，点M处为3，点N处为7，求S_△BMN：S_△BPC的值．

Answer 1

分析：（1）根据过直线外一点作该直线的垂线的作图方法，即可作出PC边上的高；
（2）由题意得：DG∥EF，推出∠APD=∠2=51°，再由∠1=30°，根据外角的性质，即可推出∠3的度数；
（3）由题意推出MN、PC的长度，再根据平行线的性质，推出△BMN与△BPC相似，然后根据相似三角形的面积比等于相似比的平方，即可推出S_△BMN：S_△BPC的值．

解答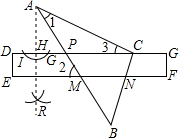：解：（1）作法：①以点A为圆心，任意长为半径画弧，设弧与直线PC交于点I、G，
②分别以点I、G为圆心大于IG为半径作弧，设两弧交于点R，
③连接AR，设AR与直线PC交于点H，
④则AH为所求作的PC边上的高，

（2）∵将三角尺的直角顶点放在直尺的一边上，
∴DG∥EF，
∴∠APD=∠2，
∵∠2=51°，
∴∠APD=51°，
∵∠1=30°，
∴∠3=∠APD-∠1=51°-30°=21°，

（3）∵EF∥DG，
∴△BMN∽△BPC，
∵直尺上点P处刻度为2，点C处为8，点M处为3，点N处为7，
∴MN=7-3=4，PC=8-2=6，
∴

S△BMN

S△BPC

=(

MN

PC

)2=

4

9

．

点评：本题主要考查过直线外一点作该直线的垂线、平行线的性质、相似三角形的判定与性质等知识点，关键在于能够充分的理解和熟练地运用相关的性质定理，认真的进行计算．