��Ŀ����
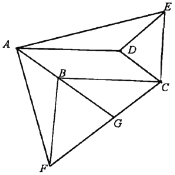
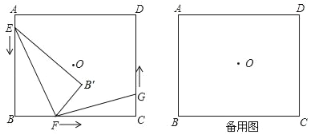
����Ŀ����ͼ����OΪ����ABCD�ĶԳ����ģ�AB��5cm��BC��6cm����E��F��G�ֱ��A��B��C����ͬʱ�������ؾ��εı߰���ʱ�뷽�������˶�����E���˶��ٶ�Ϊ1cm/s����F���˶��ٶ�Ϊ3cm/s����G���˶��ٶ�Ϊ1.5cm/s������F�����C������F���C�غϣ�ʱ����������ֹ֮ͣ�˶������˶������У���EBF����ֱ��EF�ĶԳ�ͼ������EB��F�����E��F��G�˶���ʱ��Ϊt����λ��s����
��1����t���ڶ���sʱ���ı���EBFB��Ϊ�����Σ�
��2�����Ե�E��B��FΪ��������������Ե�F��C��GΪ��������������ƣ���t��ֵ��
��3���Ƿ����ʵ��t��ʹ�õ�B�����O�غϣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��t��1.25����2����t��1.4s��t������7+![]() ��sʱ���Ե�E��B��FΪ��������������Ե�F��C��GΪ��������������ƣ���3��������ʵ��t��ʹ�õ�B�����O�غϣ����ɼ�����.
��sʱ���Ե�E��B��FΪ��������������Ե�F��C��GΪ��������������ƣ���3��������ʵ��t��ʹ�õ�B�����O�غϣ����ɼ�����.
��������
��1�����������ε����ʣ��õ�BE��BF����һԪһ�η�����⼴�ɣ�
��2����EBF���FCG���ƣ��������������Ҫ�������ۣ���һ�������㣻
��3������Ϊ���������⣮������ڣ�����Էֱ�����ڲ�ͬ�����µ�tֵ�����ǻ���ì�ܣ����Բ�����
��1�����ı���EBFB��Ϊ�����Σ���BE��BF��BE��5��t��BF��3t��
����5��t��3t��
���t��1.25��
�ʴ�Ϊ��1.25��
��2��������������������£�
������EBF�ס�FCG��
����![]() ����
����![]() ��
��
��ã�t��1.4��
������EBF�ס�GCF��
����![]() ����
����![]() ��
��
��ã�t����7��![]() ���������⣬��ȥ����t����7+
���������⣬��ȥ����t����7+![]() ��
��
�൱t��1.4s��t������7+![]() ��sʱ���Ե�E��B��FΪ��������������Ե�F��C��GΪ��������������ƣ�
��sʱ���Ե�E��B��FΪ��������������Ե�F��C��GΪ��������������ƣ�
��3���������ʵ��t��ʹ�õ�B�����O�غϣ�
��ͼ������O��OM��BC�ڵ�M������Rt��OFM�У�OF��BF��3t��FM��![]() BC��BF��3��3t��OM��2.5��
BC��BF��3��3t��OM��2.5��
�ɹ��ɶ����ã�OM2+FM2��OF2��
����2.52+��3��3t��2����3t��2
��ã�t��![]() ��
��
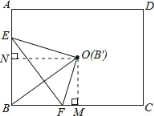
����O��ON��AB�ڵ�N������Rt��OEN�У�OE��BE��5��t��EN��BE��BN��5��t��2.5��2.5��t��ON��3��
�ɹ��ɶ����ã�ON2+EN2��OE2��
����32+��2.5��t��2����5��t��2
��ã�t��![]() ��
��
��![]() ��
��![]() ��
��
�����ʵ��t��ʹ�õ�B�����O�غϣ�