题目内容
(本题满分10分)如图,在平面直角坐标系 中,把抛物线
中,把抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左边),与
的左边),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
.
(1)写出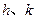 的值;
的值;
(2)判断 的形状,并说明理由;
的形状,并说明理由;
(3)在线段 上是否存在点
上是否存在点 ,使
,使
 ∽
∽ ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
解:(1) 的顶点坐标为D(-1,-4),
的顶点坐标为D(-1,-4),
∴ 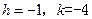 . …………………………………………2分
. …………………………………………2分
(2 )由(1)得
)由(1)得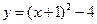 .
.
当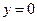 时,
时, .解之,得
.解之,得  .
.
∴ 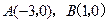 .
.
又当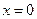 时,
时,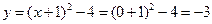 ,
,
∴C点坐标为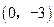 .………………………………4分
.………………………………4分
又抛物线顶点坐标 ,作抛物线的对称轴
,作抛物线的对称轴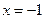 交
交 轴于点E,
轴于点E, 轴于点
轴于点 .易知
.易知
在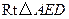 中,
中, ;
;
在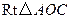 中,
中,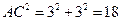 ;
;
在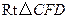 中,
中,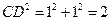 ;
;
∴ 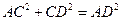 .
.
∴ △ACD是直角 三角形.…………………………6分
三角形.…………………………6分
(3)存在.作OM∥BC交AC于M,M点即为所求点.
由(2)知,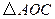 为等腰直角三角形,
为等腰直角三角形,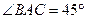 ,
,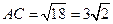 .
.
由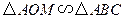 ,得
,得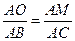 .
.
即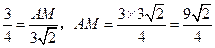 . …………………………8分
. …………………………8分
过 点作
点作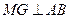 于点
于点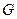 ,则
,则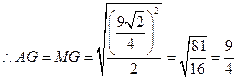 ,
,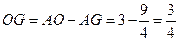 .
.
又点M 在第三象限,所以
在第三象限,所以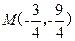 . …………………………10分
. …………………………10分
解析

练习册系列答案
相关题目

 的图象的顶点为
的图象的顶点为 .二次函数
.二次函数 的图象与
的图象与 轴交于原点
轴交于原点 及另一点
及另一点 ,它的顶点
,它的顶点 在函数
在函数
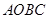 为菱形时,求函数
为菱形时,求函数 与支架
与支架 所在直线相交于水箱横断面
所在直线相交于水箱横断面 的圆心
的圆心 ,支架
,支架 垂直,
垂直, 厘米,
厘米,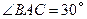 ,另一根辅助支架
,另一根辅助支架 厘米,
厘米, .
. 的长度.(结果保留三个有效数字,参考数据:
的长度.(结果保留三个有效数字,参考数据: )
)


