��Ŀ����
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ������������
������������![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ����յ�
����λ���ȵ��ٶ����յ�![]() �˶�������
�˶�������![]() �����
�����![]() ��
��![]() �غ�ʱ���ڱ�
�غ�ʱ���ڱ�![]() ��ȡһ��
��ȡһ��![]() ������
������![]() ������
������![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��������
��������![]() .���
.���![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ��.
��.
��1���ú�![]() �Ĵ���ʽ��ʾ�߶�
�Ĵ���ʽ��ʾ�߶�![]() �ij�;
�ij�;
��2��������![]() Ϊ������ʱ����
Ϊ������ʱ����![]() ��ֵ;
��ֵ;
��3�������![]() ��
��![]() �ص�����ͼ�ε��ܳ�Ϊ
�ص�����ͼ�ε��ܳ�Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ;
֮��ĺ�����ϵʽ;
��4������![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ������
������![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() .��
.��![]() ��
��![]() ��������ֻ��һ�����ھ���
��������ֻ��һ�����ھ���![]() �ڲ�ʱ��ֱ��д����ʱ
�ڲ�ʱ��ֱ��д����ʱ![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
���𰸡���1����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ����2��������
����2��������![]() Ϊ������ʱ��
Ϊ������ʱ��![]() ��ֵΪ
��ֵΪ![]() ����3����
����3����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ�� ![]() ����4��
����4��![]() ��
��![]() .
.
��������
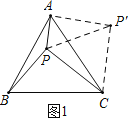
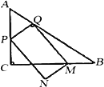
��1������P��AC��ʱ���ӳ�AC����D��ʹ��CD=AC���á�ABD=2��ABC=��PQA���ɵ�PQ��DB���á�APQ�ס�ADB���������������εĶ�Ӧ�߳ɱ����г���ʽ���μ��ɵó����ۣ�
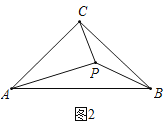
����P��CB��ʱ������Q��QE��BC���ɡ�PQA=2��B����������ǵ����ʿɵá�QPBΪ���������Σ����ݡ����ߺ�һ���ɵ�BE=![]() BP=
BP=![]() (7-t)��Ȼ���ɡ�BQE�ס�BAC�г�����ʽ���ɵó����ۣ�
(7-t)��Ȼ���ɡ�BQE�ס�BAC�г�����ʽ���ɵó����ۣ�
��2������P��AC��ʱ����P��QG��AC��QH��BC���ɣ�1���ɵá�AQP�ǵ��������Σ��ɵ�GP=![]() t�����ݾ��ε��ж����ı���GQHCΪ���Σ��ó�QH=GC=3-
t�����ݾ��ε��ж����ı���GQHCΪ���Σ��ó�QH=GC=3-![]() t������Բ�ڽ��ı��εĶԽǻ����͵��������ε����ʵó���A=��QMH�������ɵá�QHM�ס�BCA���������������ε������г�����ʽ���QM����QM=PQ�������t����P��BC��ʱ�����ܹ��������Σ����ϼ��ɵó����ۣ�
t������Բ�ڽ��ı��εĶԽǻ����͵��������ε����ʵó���A=��QMH�������ɵá�QHM�ס�BCA���������������ε������г�����ʽ���QM����QM=PQ�������t����P��BC��ʱ�����ܹ��������Σ����ϼ��ɵó����ۣ�
��3������P��AC��ʱ���á�CPK=��KMN=��B���������Ǻ��������PK��MK��ֵ��Ȼ��������PQ+QM+MK+PK���ɣ�
����P��BC��ʱ���ɣ�1���ɵá�QPM=��B����Rt��QPM�У��������Ǻ��������QM��PM�ij���Ȼ�������㼴�ɣ�
��4������P��AC��ʱ������A��AD��PQ������C��CE��PN���ֵ�A���ھ���PQMN�ڲ�����C�䲻�ھ���PQMN�ڲ��͵�A�䲻�ھ���PQMN�ڲ�����C���ھ���PQMN�ڲ�����![]() ��
��![]() ����������t�ķ�Χ������P��BC��ʱ����Ȼ��A��͵�C�䶼�ھ���PQMN�ⲿ��
����������t�ķ�Χ������P��BC��ʱ����Ȼ��A��͵�C�䶼�ھ���PQMN�ⲿ��
�⣺��1������P��AC��ʱ����0��t��3ʱ���ӳ�AC����D��ʹ��CD=AC��
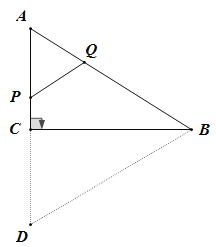
��Rt��ABC��AC=3��BC=4��
��AB=5��
�ڡ�ABC�͡�DBC�У�
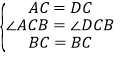 ��
��
���ABC�ա�DBC��SAS����
��AC=CD=3��AB=CD=5����ABC=��DBC��
�ߡ�PQA=2��ABC��
���PQA=��ABD��
��PQ��BD��
���APQ�ס�ADB��
��![]() ��
��
��![]() ��
��
��PQ=![]() ��
��
����P��CB��ʱ����3��t��7ʱ��
����Q��QE��BC�ڵ�E��
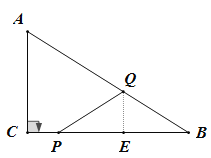
�ߡ�PQA=��B+��QPB����PQA=2��B��
���QPB=��B��
��PQ=QB��
��BE=![]() PB=
PB=![]() (7-t)��
(7-t)��
�ߡ�C=90�㣬
��QE��AC��
��![]() ��
��
��![]() ��
��
��ã�QB=![]() ��
��
��PQ=![]() ��
��
���ϣ���![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() .
.
��2����![]() ʱ����ͼ�٣�
ʱ����ͼ�٣�
����![]() ��QG��AC�ڵ�G��
��QG��AC�ڵ�G��![]() �ڵ�
�ڵ�![]() .
.
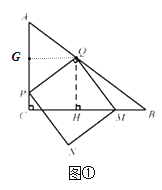
�ɣ�1���ɵ�AQ=PQ��
���A=��APQ��AG=GP=![]() AP=
AP=![]() t��
t��
��CG=AC-AG=3-![]() t��
t��
�ߡ�QGC=��C=��QHC=90�㣬
���ı���QGCHΪ���Σ�
��QH=CG=3-![]() t��
t��
�ߡ�C=��PQM=90�㣬
���APQ=��QMH��
���A=��QMH��
�ߡ�QHM=��C=90�㣬
���QHM�ס�BCA��
��![]() ��
��
��![]() ��
��
��![]() .
.
������![]() Ϊ������ʱ��
Ϊ������ʱ��
![]() .
.
���![]() .
.
��![]() ʱ������
ʱ������![]() ������Ϊ������.
������������.
�൱����![]() Ϊ������ʱ��
Ϊ������ʱ��![]() ��ֵΪ
��ֵΪ![]() .
.
��3����![]() ʱ����ͼ�ڣ�
ʱ����ͼ�ڣ�
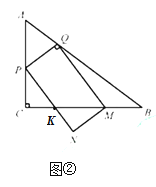
�ɣ�1���ɵá�CPK=��KMN=��B��
��Rt��PCK��
PK=![]() =
=![]() =
=![]() ��
��
��Rt��KNM��
MK=![]() =
=![]() ��
��
![]() .
.
��![]() ʱ����ͼ�ۣ�
ʱ����ͼ�ۣ�

�ɣ�1���ɵá�QPM=��B��
��Rt��QPM��
QM=PQtan��QPM=![]() ��
��
PM=![]() =
=![]() =
=![]() ��
��
![]() .
.
��4������P��AC��ʱ��0��t��3��
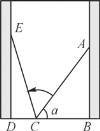
����A��AD��PQ�ڵ�D������C��CE��PN�ڵ�E����ͼ��ʾ��
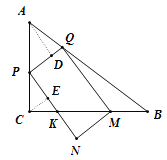
�ɣ�1���á�APQ=��PCE=��BAC��
��Rt��ADP��AD=APsin��APQ=![]() ��
��
��Rt��PCE��CE=CPcos��PCE=![]() ��
��
����A���ھ���PQMN�ڲ�����C�䲻�ھ���PQMN�ڲ�ʱ��
![]() ��
��
��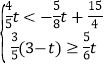 ��
��
��ã�t��![]() ��
��
��0��t��![]() ��
��
����A�䲻�ھ���PQMN�ڲ�����C���ھ���PQMN�ڲ�ʱ��
![]() ��
��
��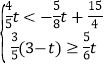 ��
��
��ã�t��![]() ��
��
��![]() ��t��3��
��t��3��
����P��BC��ʱ����Ȼ��A��͵�C�䶼�ھ���PQMN�ⲿ��
��![]() ��
��![]() .
.