题目内容
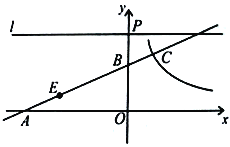
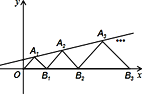
【题目】如图,在平面直角坐标系中,点A1,A2,A3,… 和B1,B2,B3,… 分别在直线![]() 和x轴上.△OA1 B1,△B1 A2 B2,△B2 A3 B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是( )
和x轴上.△OA1 B1,△B1 A2 B2,△B2 A3 B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
因为每个A点为等腰直角三角形的直角顶点,则每个点A的纵坐标为对应等腰直角三角形的斜边一半.故先设出各点A的纵坐标,可以表示A的横坐标,代入解析式可求点A的纵坐标,规律可求.
分别过点A1,A2,A3,…向x轴作垂线,垂足为C1,C2,C3,…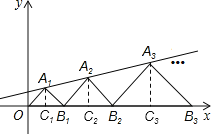
∵点A1(1,1)在直线y=![]() x+b上
x+b上
∴代入求得:b=![]()
∴y=![]()
∵△OA1B1为等腰直角三角形
∴OB1=2
设点A2坐标为(a,b)
∵△B1A2B2为等腰直角三角形
∴A2C2=B1C2=b
∴a=OC2=OB1+B1C2=2+b
把A2(2+b,b)代入y=![]()
解得b=![]()
∴OB2=5
同理设点A3坐标为(a,b)
∵△B2A3B3为等腰直角三角形
∴A3C3=B2C3=b
∴a=OC3=OB2+B2C3=5+b
把A3(5+b,b)代入y=![]()
解得b=![]()
以此类推,发现每个A的纵坐标依次是前一个的![]() 倍
倍
则A2019的纵坐标是(![]() )2018
)2018
故选:B

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
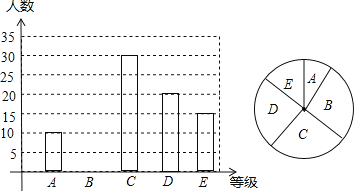
启东小题作业本系列答案【题目】2019年,我省中考体育分值增加到55分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
成绩 | 3′40″及以下 | 3′41~4′ | 4′01″~4′20′ | 4′21″~4′40″ | 4′41″及以上 |
等级 | A | B | C | D | E |
百分比 | 10% | 25% | m | 20% | n |
(1)求样本容量及表格中的m和n的值
(2)求扇形统计图中A等级所对的圆心角度数,并补全统计图.
(3)我校9年级共有女生500人.若女生八百米成绩的达标成绩为4分,我校九年级女生八百米成绩达标的人数有多少?