题目内容
【题目】如图,已知一次函数y=﹣ ![]() x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA. 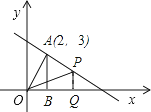
(1)求此一次函数的解析式;
(2)设点P为直线y=﹣ ![]() x+b上的一点,且在第一象限内,经过P作x轴的垂线,垂足为Q.若S△POQ=
x+b上的一点,且在第一象限内,经过P作x轴的垂线,垂足为Q.若S△POQ= ![]() S△AOB , 求点P的坐标.
S△AOB , 求点P的坐标.
【答案】
(1)
解:∵一次函数y=﹣ ![]() x+b的图象经过点A(2,3),
x+b的图象经过点A(2,3),
∴3=(﹣ ![]() )×2+b,
)×2+b,
解得b=4,
故此一次函数的解析式为:y=﹣ ![]() x+4
x+4
(2)
解:设P(p,d),p>0,
∵点P在直线y=﹣ ![]() x+4的图象上,
x+4的图象上,
∴d=﹣ ![]() p+4①,
p+4①,
∵S△POQ= ![]() S△AOB=
S△AOB= ![]() ×
× ![]() ×2×3,
×2×3,
∴ ![]() pd=
pd= ![]() ②,
②,
①②联立得, 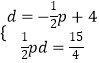 ,
,
解得 ![]() 或
或 ![]() ,
,
∴P点坐标为:(3, ![]() )或(5,
)或(5, ![]() )
)
【解析】(1)直接把点A(2,3)代入一次函数y=﹣ ![]() x+b即可求出b的值,进而得出一次函数的解析式;(2)设P(p,d),p>0,再根据点P在一次函数的图象上及S△POQ=
x+b即可求出b的值,进而得出一次函数的解析式;(2)设P(p,d),p>0,再根据点P在一次函数的图象上及S△POQ= ![]() S△AOB , 即可得出关于p、d的方程组,求出p、d的值即可.
S△AOB , 即可得出关于p、d的方程组,求出p、d的值即可.
【考点精析】关于本题考查的确定一次函数的表达式,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能得出正确答案.

练习册系列答案
相关题目
【题目】某个体水果店经营某种水果,进价![]() 元/千克,售价
元/千克,售价![]() 元/千克,
元/千克,![]() 月
月![]() 日至
日至![]() 月
月![]() 日经营情况如下表:
日经营情况如下表:
日期 |
|
|
|
|
|
购进 |
|
|
|
|
|
售出 |
|
|
|
|
|
损耗 |
|
|
|
|
|
![]() 若
若![]() 月
月![]() 日的库存为
日的库存为![]() ,则
,则![]() 月
月![]() 日的库存为________;
日的库存为________;
![]() 就
就![]() 月
月![]() 日经营情况看,当天是赚还是赔了?
日经营情况看,当天是赚还是赔了?
![]() 每天交卫生费
每天交卫生费![]() 元,则
元,则![]() 月
月![]() 日
日![]() 月
月![]() 日该个体户共赚多少钱?
日该个体户共赚多少钱?