题目内容
【题目】如图,在直角坐标系中,已知点A(-8,0),B(0,6),点M在线段AB上。
(1)如图1,如果点M是线段AB的中点,且⊙M的半径等于4,试判断直线OB与⊙M的位置关系,并说明理由;
(2)如图2,⊙M与x轴,y轴都相切,切点分别为E,F,试求出点M的坐标;
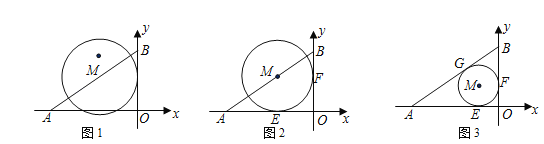
(3)如图3,⊙M与x轴,y轴,线段AB都相切,切点分别为E,F,G,试求出点M的坐标(直接写出答案)
【答案】(1)OB与⊙M相切;(2)M(-![]() ,
,![]() );(3)M(-2,2)
);(3)M(-2,2)
【解析】(1)设线段OB的中点为D,连结MD,根据三角形的中位线求出MD,根据直线和圆的位置关系得出即可;
(2)求出过点A、B的一次函数关系式是y=![]() x+6,设M(a,﹣a),把x=a,y=﹣a代入y=
x+6,设M(a,﹣a),把x=a,y=﹣a代入y=![]() x+6得出关于a的方程,求出即可.
x+6得出关于a的方程,求出即可.
(3)连接ME、MF、MG、MA、MB、MO,设ME=MF=MG=r,根据S△ABC=![]() AOME+
AOME+![]() BOMF+
BOMF+![]() ABMG=
ABMG=![]() AOBO求得r=2,据此可得答案.
AOBO求得r=2,据此可得答案.
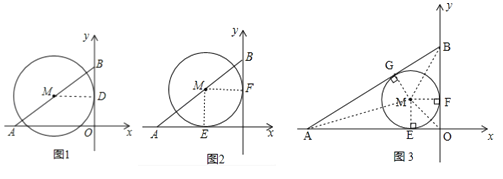
(1)直线OB与⊙M相切.理由如下:
设线段OB的中点为D,如图1,连结MD,
∵点M是线段AB的中点,所以MD∥AO,MD=4,
∴∠AOB=∠MDB=90°,∴MD⊥OB,点D在⊙M上.
又∵点D在直线OB上,∴直线OB与⊙M相切;
(2)如图2,连接ME,MF,
∵A(﹣8,0),B(0,6),∴设直线AB的解析式是y=kx+b,∴![]() ,解得:k=
,解得:k=![]() ,b=6,即直线AB的函数关系式是y=
,b=6,即直线AB的函数关系式是y=![]() x+6.
x+6.
∵⊙M与x轴、y轴都相切,∴点M到x轴、y轴的距离都相等,即ME=MF,设M(a,﹣a)(﹣8<a<0),把x=a,y=﹣a代入y=![]() x+6,得:﹣a=
x+6,得:﹣a=![]() a
a![]() ,∴点M的坐标为(﹣
,∴点M的坐标为(﹣![]() ).
).
(3)如图3,连接ME、MF、MG、MA、MB、MO,
∵⊙M与x轴,y轴,线段AB都相切,∴ME⊥AO、MF⊥BO、MG⊥AB,设ME=MF=MG=r,则S△ABC=![]() AOME+
AOME+![]() BOMF+
BOMF+![]() ABMG=
ABMG=![]() AOBO.
AOBO.
∵A(﹣8,0),B(0,6),∴AO=8、BO=6,AB=![]() =10,∴
=10,∴![]() r8+
r8+![]() r6+
r6+![]() r10=
r10=![]() ×6×8,解得:r=2,即ME=MF=2,∴点M的坐标为(﹣2,2).
×6×8,解得:r=2,即ME=MF=2,∴点M的坐标为(﹣2,2).

【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.