题目内容
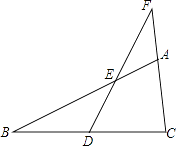
【题目】己知:在等腰三角形ABC中,AB=AC,AD⊥BC于点D,以AC为边作等边三角形ACE,直线BE交直线AD于点F,连接FC.
(1)如图1,120°<∠BAC<180°,△ACE与△ABC在直线AC的异侧,且FC交AE于点M.
①求证:∠FEA=∠FCA;
②猜想线段FE,FA,FD之间的数量关系,并证明你的结论:
(2)当60°<∠BAC<120°,且△ACE与△ABC在直线AC的同侧时,利用图2画出图形探究线段FE,FA,FD之间的数量关系,并直接写出你的结论.
【答案】
(1)
解:①∵AD⊥BC,AB=AC,
∴BD=DC,
∴FB=FC,
∴∠FBC=∠FCB,
∴AB=AC,
∴∠ABC=∠ACB,
∵∠FBA=∠FCA,
∵以AC为边作等边三角形ACE,
∴AE=AC=AB,
∴∠ABF=∠AEF,
∴∠ACF=∠AEF,
即:∠FEA=∠FCA;
②结论:EF=FA+AD,
∵以AC为边作等边三角形ACE,
∴∠EAC=60°,
由①有,∠ACF=∠AEF,
∴∠EFC=∠EAC=60°,
由①得,BF=CF,FD⊥BC,
∴∠BFD=∠CFD,
∵∠BFD+∠CFD+∠EFC=180°,
∴∠BFD=∠CFD= ![]() =60°,
=60°,
∴∠FCD=90°﹣∠CFD=30°,
∴∠ACD+∠ACF=30°,
∴∠ECF=∠ECA﹣∠ACF=60°﹣∠ACF=60°﹣(30°﹣∠ACD)=30°+∠ACD,
如图1,

延长AD,在AD上截取AD=DK,连接CK,
∵AD⊥BC,
∴∠ACD=∠KCD,CA=CK
∴∠FCK=∠FCD+∠KCD=∠ACF+∠ACD+∠KCD=30°+∠KCD=30°+∠ACD,
∴∠FCK=∠ECF,
∵AC=CE,AC=CK,
∴CK=CE,
在△CFE和△CFK中, 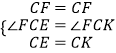 ,
,
∴△CFE≌△CFK,
∴FE=FK=FD+DK,
∵AD=DK,
∴FE=FD+AD;
(2)
解:结论:EF=FA+AD,
如图2,

∵以AC为边作等边三角形ACE,
∴∠EAC=60°,
同(2)①的方法有,∠ACF=∠AEF,
∴∠EFC=∠EAC=60°,
同(2)①方法得,BF=CF,FD⊥BC,
∴∠BFD=∠CFD,
∵∠BFD+∠CFD+∠EFC=180°,
∴∠BFD=∠CFD= ![]() =60°,
=60°,
∴∠FCD=90°﹣∠CFD=30°,
∴∠ACD﹣∠ACF=30°,
∴∠ECF=∠ECA+∠ACF=60°+∠ACF=60°+(∠ACD﹣30°)=30°+∠ACD,
延长AD,在AD上截取AD=DK,连接CK,
∵AD⊥BC,
∴∠ACD=∠KCD,CA=CK
∴∠FCK=∠FCD+∠KCD=∠ACD﹣∠ACF+∠KCD=30°+∠KCD=30°+∠ACD,
∴∠FCK=∠ECF,
∵AC=CE,AC=CK,
∴CK=CE,
在△CFE和△CFK中, 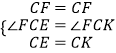 ,
,
∴△CFE≌△CFK,
∴FE=FK=FD+DK,
∵AD=DK,
∴FE=FD+AD;
【解析】(1)①利用中垂线得到∠FBC=∠FCB,从而得到∠FBA=∠FCA,再由等边三角形的性质得到∠ABF=∠AEF即可;②先得到∠EFC=∠EAC=60°,从而判断出∠ACD+∠ACF=30°,进而得出∠FCK=∠ECF,判断出△CFE≌△CFK,即可;(2)先得到∠EFC=∠EAC=60°,从而判断出∠ACD﹣∠ACF=30°,进而得出∠FCK=∠ECF,判断出△CFE≌△CFK,即可;
【考点精析】关于本题考查的三角形三边关系,需要了解三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边才能得出正确答案.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案