题目内容
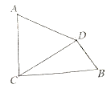
【题目】如图,AC⊥BC,垂足为C,AC=6,BC=4![]() ,将线段AC绕点C按顺时针方向旋转60°,得到线段CD,连接AD,DB。
,将线段AC绕点C按顺时针方向旋转60°,得到线段CD,连接AD,DB。
(1)求线段BD的长度;
(2)求四边形ACBD的面积.
【答案】(1)![]() ; (2)
; (2)![]()
![]() .
.
【解析】
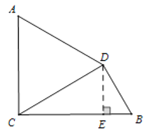
(1)由旋转可得△ACD是等边三角形,过点D作DE⊥BC于点E,在Rt△CDE中,分别求得DE,CE的长,再由勾股定理在Rt△ BDE中求得BD的长.(2)四边形ACBD的面积可分为梯形ACED和三角形DEB的面积.
解:
(1)由旋转得AC=CD=6,∠ACD=60°,
∴△ACD是等边三角形,
过点D作DE⊥BC于点E,
∵AC⊥BC,
∴∠DCE=∠ACB-∠ACD=90°-60°=30°
∴在Rt△CDE中,
![]() ,
,
![]() ,
,
∴ ![]() .
.
∴ Rt△ BDE中,
![]() .
.
(2)S四边形ACBD= S梯形ACED+ S△EBD,
=![]() ,
,
=![]() ,
,
![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目