题目内容
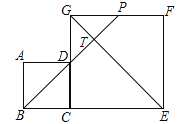
【题目】如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 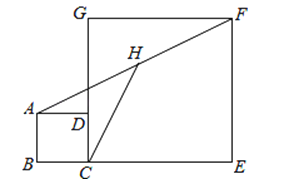
【答案】![]()
【解析】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,
∴AB=BC=1,CE=EF=3,∠E=90°,
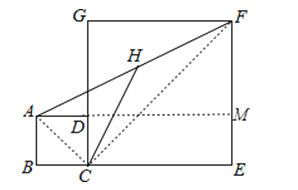
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=![]() AF,
AF,
在Rt△AMF中,由勾股定理得:AF=![]() =
=![]() =2
=2![]() ,
,
∴CH=![]() ,
,
所以答案是:![]() .
. 
【考点精析】利用正方形的性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目