题目内容
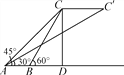
【题目】如图，两个观察者从A，B两地观测空中C处一个气球，分别测得仰角为45°和60°.已知A，B两地相距100 m．当气球沿与AB平行的路线飘移20 s后到达点C′，在A处测得气球的仰角为30°.求：
(1)气球飘移的平均速度(精确到0.1 m/s)；
(2)在B处观测点C′的仰角(精确到度)．
【答案】（1）气球飘移的平均速度为8.7 m/s；（2）在B处观测点C′的仰角为37°.
【解析】试题首先分析图形：根据题意构造直角三角形；本题涉及到两个直角三角形，应利用其公共边构造等量关系，进而可求出答案．
试题解析：解：（1）作CD⊥AB，C1E⊥AB，垂足分别为D、E．在Rt△ACD中，AD=CD÷tan∠CAD=CD÷tan45°=CD；在Rt△BCD中，BD=CD÷tan∠CBD=CD÷tan60°=
；
又因为AB=AD﹣BD=200，所以CD﹣=200，解得：CD=100（3
），又CD⊥AB，C1E⊥AB，CC1∥AB，所以C1E=CD，DE=CC1．在Rt△AEC1中，AE=C1E÷tan∠C1AE=100（3+
）÷tan30°=300（
），所以CC1=DE=AE﹣AD=300（）﹣100（3+），即CC1=200，速度为200÷40≈8.66m/s；
（2）由（1）知BD==100（1），所以tan∠C1BE=
=
≈0.7637，所以∠C1BE=37°，即仰角为37°．
练习册系列答案
相关题目
