题目内容
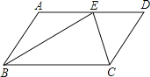
【题目】如图，在ABCD中，AD＝12cm，CD＝6cm，E为AD上一点，且BE＝BC，CE＝CD，则DE＝__cm．
【答案】3.
【解析】
先根据平行四边形的性质得出∠2=∠3，再根据BE=BC，CE=CD，∠1=∠2，∠3=∠D，进而得出∠1=∠2=∠3=∠D，故可得出△BCE∽△CDE，再根据相似三角形的对应边成比例即可得出结论．
解：如图：
∵四边形ABCD是平行四边形，AD=12cm，CD=6cm，
∴BC=AD=12cm，AD∥BC，
∴∠2=∠3，
∵BE=BC，CE=CD，
∴BE=BC=12cm，CE=CD=6cm，∠1=∠2，∠3=∠D，
∴∠1=∠2=∠3=∠D，
∴△BCE∽△CDE，
∴
，
解得：DE=3；
故答案为：3.
练习册系列答案
相关题目
