Question

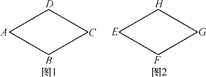
【题目】如图，在等边三角形ABC中，顶点A，C处各有一只蚂蚁，它们同时出发，分别以同样的速度由A向B和由C向A爬行，经过t秒后，它们分别到达D，E处，请问两只蚂蚁在爬行过程中，

(1)CD与BE有何数量关系，为什么？

(2)DC与BE相交所成的∠BFC的大小是否发生变化？若有变化，请说明理由；若没有变化，求出∠BFC的大小。

Answer 1

【答案】（1）CD=BE，理由见解析；（2）∠BFC的大小不变，始终为120°

【解析】试题分析：（1）证明△ACD≌△CBE即可证明CD=BE；（2）要求∠BFC的度数即要求∠FBC和∠FCB的和，即要求∠FCB和∠ACD的度数之和，即为∠ACB的度数，为60°，因此可得出∠BFC=120°，保持不变.

试题解析：

（1）CD=BE，

∵两只蚂蚁同时出发，同样的速度，

∴AD=CE，

又 ∵△ABC是等边三角形，

∴AC=BC ，∠A=∠BCE=60°，

∵在△ACD和△CBE中

，

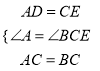∴△ACD≌△CBE (SAS)，

∴CD=BE；

（2）∠BFC 大小不会发生变化，

∵△ACD≌△CBE，

∴∠DCA=∠EBC，

又∵∠DCA+∠DCB=60°，

∴∠EBC+∠DCB=60°，

∴∠BFC=180°-60°=120°，

∴∠BFC的大小不变，始终为120°.