题目内容
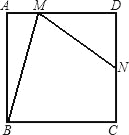
【题目】在正方形ABCD中,N是DC的中点,M是AD上异于D的点,且∠NMB=∠MBC,则tan∠ABM=_____.
【答案】![]()
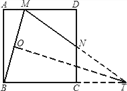
【解析】根据∠NMB=∠MBC,延长MN,BC相交于T,得到等腰△TBM,连接点T和MB的中点,得到相似三角形,然后由相似三角形的性质进行计算,求出∠ABM的正切.
如图:延长MN交BC的延长线于T,设MB的中点为O,连TO,则OT⊥BM,
∵∠ABM+∠MBT=90°,
∠OTB+∠MBT=90°,
∴∠ABM=∠OTB,则△BAM∽△TOB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,即MB2=2AMBT ①
,即MB2=2AMBT ①
令DN=1,CT=MD=K,则:AM=2﹣K,BM=![]() ,BT=2+K,
,BT=2+K,
代入①中得:4+(2﹣K)2=2(2﹣K)(2+K),
解方程得:K1=0(舍去),K2=![]() .
.
∴AM=2﹣![]() =
=![]() .
.
tan∠ABM=![]() =
=![]() =
=![]() .
.
故答案是:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某校要从王同学和李同学中挑选一人参加县知识竞赛在五次选拔测试中他俩的成绩如下表.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
王同学 | 60 | 75 | 100 | 90 | 75 |
李同学 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
王同学 | 80 | 75 | 75 | _____ |
李同学 |
|
|
|
|
(2)在这五次测试中,成绩比较稳定的同学是谁若将80分以上(含80分)的成绩视为优秀,则王同学、李同学在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.