题目内容
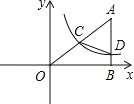
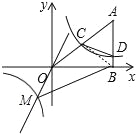
【题目】如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式;
(2)若函数y=3x与y=![]() 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
【答案】(1)反比例函数解析式为:y=![]() ;
;
(2)![]()
【解析】
试题分析:(1)先根据锐角三角函数的定义,求出OA的值,然后根据勾股定理求出AB的值,然后由C点是OA的中点,求出C点的坐标,然后将C的坐标代入反比例函数y=![]() 中,即可确定反比例函数解析式;
中,即可确定反比例函数解析式;
(2)先将y=3x与y=![]() 联立成方程组,求出点M的坐标,然后求出点D的坐标,然后连接BC,分别求出△OMB的面积,△OBC的面积,△BCD的面积,进而确定四边形OCDB的面积,进而可求三角形OMB与四边形OCDB的面积的比.
联立成方程组,求出点M的坐标,然后求出点D的坐标,然后连接BC,分别求出△OMB的面积,△OBC的面积,△BCD的面积,进而确定四边形OCDB的面积,进而可求三角形OMB与四边形OCDB的面积的比.
试题解析:(1)∵A点的坐标为(8,y),∴OB=8,∵AB⊥x轴于点B,sin∠OAB=![]() ,
,
∴![]() ,∴OA=10,由勾股定理得:AB=
,∴OA=10,由勾股定理得:AB=![]() ,
,
∵点C是OA的中点,且在第一象限内,∴C(4,3),∵点C在反比例函数y=![]() 的图象上,
的图象上,
∴k=12,∴反比例函数解析式为:y=![]() ;
;
(2)将y=3x与y=![]() 联立成方程组,得:
联立成方程组,得: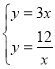 ,
,
解得: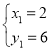 ,
, ,
,
∵M是直线与双曲线另一支的交点,∴M(﹣2,﹣6),∵点D在AB上,∴点D的横坐标为8,
∵点D在反比例函数y=![]() 的图象上,∴点D的纵坐标为
的图象上,∴点D的纵坐标为![]() ,∴D(8,
,∴D(8,![]() ),∴BD=
),∴BD=![]() ,
,
连接BC,如图所示,∵S△MOB=![]() 8|﹣6|=24,S四边形OCDB=S△OBC+S△BCD=
8|﹣6|=24,S四边形OCDB=S△OBC+S△BCD=![]() 83+
83+![]() =15,
=15,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目