题目内容
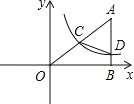
【题目】如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.你能判断DF与AB的位置关系吗?请说明理由.
【答案】证明:平行,
理由是:∵BE是∠ABC的角平分线
∴∠1=∠2,
∵∠E=∠1,
∴∠E=∠2,
∴AE∥BC,
∴∠A+∠ABC=180°,
∵∠3+∠ABC=180°,
∴∠A=∠3,
∴DF∥AB.
【解析】由BE是∠ABC的角平分线,得∠1=∠2,根据∠E=∠1,得∠E=∠2,从而得出AE∥BC,即∠A+∠ABC=180°,根据∠3+∠ABC=180°得∠A=∠3,即可证明DF∥AB.
【考点精析】关于本题考查的平行线的判定,需要了解同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行才能得出正确答案.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目