��Ŀ����
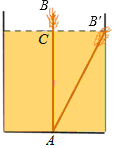
����Ŀ����ͼ1��AB��CD����E��F�ֱ���ֱ��CD��AB�ϣ���BEC��2��BEF������A��AG��BE���ӳ��߽��ڵ�G����CD�ڵ�N��AKƽ�֡�BAG����EF�ڵ�H����BE�ڵ�M��
��1��ֱ��д����AHE����FAH����KEH֮��Ĺ�ϵ��________��
��2������BEF��![]() ��BAK�����AHE��
��BAK�����AHE��
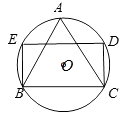
��3����ͼ2���ڣ�2���������£�����KHE���ŵ�E��ÿ��5�����ٶ���ʱ����ת����תʱ��Ϊt����KE��������ED�غ�ʱֹͣ��������ת�����У�����KHE������һ�����ENG��ijһ��ƽ��ʱ��ֱ��д����ʱt��ֵ��

���𰸡���1����AHE=��KEH+��FAH����2��75������3��t=6��12��21��24��30��
��������
��1������ƽ���ߵ����ʺ������ε�������ʿɵô𰸣�
��2�����BEF=x����x�ֱ��ʾ����BAK����BEC����BAK����KAG����AME�͡�AHE������AG��BE���ù���x�ķ��̣����x��ֵ��������ɽ⣻
��3���ɣ�2���ɵã���KHE=105�����ٷ�4������з�����⼴�ɣ��ٵ�KH��ENʱ���ڵ�kE��GNʱ���۵�HE��GNʱ���ܵ�HK��GNʱ��
�⣺��1����AB��CD
���KEH=��AFH
�ߡ�AHE=��AFH+��FAH
���AHE=��KEH+��FAH
�ʴ�Ϊ�� ��AHE=��KEH+��FAH
��2�����BEF=x
�ߡ�BEF= ![]() ��BAK����BEC=2��BEF
��BAK����BEC=2��BEF
���BAK=��BEC=2x
��AKƽ�֡�BAG
���BAK=��KAG=2x
�ɣ�1���Ľ��ۿɵã���AME=2x+2x=4x����AHE=2x+3x=5x
��AG��BE
���G=90��
���AME+��KAG=2x+4x=90��
��x=15��
���AHE=5x=75����
��3���ɣ�2���ɵã���KHE=105������BEF=15������HEK=45������NEG=30������ENG=60��
�ٵ�KH��NGʱ
5���t=60��-30��=30��
��t=6
�ڵ�KE��GNʱ
5���t=60��
��t=12
�۵�HE��GNʱ
5���t=45��+60��=105��
��t=21
�ܵ�HK��EGʱ��
5���t=180��-30��-30��=120��
��t=24
�ݵ�HK��ENʱ��5t=150��
��t=30
����������t��ֵΪ��6��12��21��24��30��

 ��У����ϵ�д�
��У����ϵ�д�