题目内容
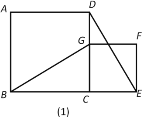
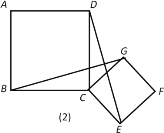
【题目】如图(1),正方形ABCD和正方形CEFG有一公共点C,且B,C,E在同一直线,连接BG,DE.
(1)请你猜想BG,DE的位置关系和数量关系,并说明理由.
(2)若正方形CEFG绕点C按顺时针方向旋转一个角度后,如图(2),BG和DE是否还存在上述关系,并说明理由.
【答案】(1)BG⊥DE,BG=DE;(2)BG与DE仍具有上述关系,即BG⊥DE,BG=DE
【解析】
(1)由四边形ABCD,CEFG都是正方形,得到CB=CD,CG=CE,∠BCG=∠DCE=90°,于是Rt△BCG≌Rt△DCE,得到BG=DE,∠CBG=∠CDE,根据三角形内角和定理可得到∠DHG=∠GCB=90°,即BG⊥DE.
(2)BG和DE还有上述关系.证明的方法与(1)一样.
解:(1)BG⊥DE,BG=DE
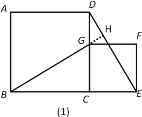
理由:如图(1),延长BG交DE于点H
∵四边形ABCD,CEFG都是正方形,
∴CB=CD,CG=CE,∠BCG=∠DCE=90°,
∴Rt△BCG≌Rt△DCE,
∴BG=DE,∠CBG=∠CDE,
而∠BGC=∠DGH,
∴∠DHG=∠GCB=90°,
即BG⊥DE.
∴BG=DE,BG⊥DE;
(2)BG与DE仍具有上述关系,即BG⊥DE,BG=DE
理由:如图(2),设BG与DC交于点M,与DE交于点H.
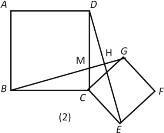
与(1)一样可证明△BCG≌△DCE,

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目