题目内容
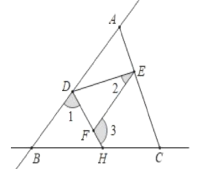
【题目】如图所示,已知OB,OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
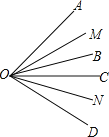
(1)若∠BOC=25°,∠MOB=15°,∠NOD=10°,求∠AOD的大小;
(2)若∠AOD=75°,∠MON=55°,求∠BOC的大小;
(3)若∠AOD=α,∠MON=β,求∠BOC的大小(用含α,β的式子表示).
【答案】(1)∠AOD= 75°;(2)∠BOC=35°;(3)![]() .
.
【解析】
(1)利用角平分线的定义可得∠AOB=2∠MOB=30°,∠COD=2∠NOD=20°,然后利用∠AOD=∠AOB+∠BOC+∠COD,可得结果;
(2)由角的加减可得∠AOM+∠DON的度数,从而求得∠BOM+∠CON,再利用∠BOC=∠MON-(∠BOM+∠CON)可得结果;
(3)由OM与ON分别为角平分线,利用角平分线的定义得到两对角相等,根据∠BOC=∠MON-∠BOM-∠CON,等量代换即可表示出∠BOC的大小.
解:(1)∵OM平分∠AOB,ON平分∠COD
∴∠AOB=2∠MOB=30°,∠COD=2∠NOD=20°
∴∠AOD=∠AOB+∠BOC+∠COD=30°+25°+20°=75°
(2)∵∠AOD=75°,∠MON=55°,
∴∠AOM+∠DON=∠AOD-∠MON=20°,
∵∠BOM+∠CON=∠AOM+∠DON=20°,
∴∠BOC=∠MON-(∠BOM+∠CON)=55°-20°=35°,
(3)∵OM平分∠AOB,ON平分∠COD,
∴∠AOM=∠BOM=![]() ∠AOB,∠CON=∠DON=
∠AOB,∠CON=∠DON=![]() ∠COD,
∠COD,
∵∠BOC=∠MON-∠BOM-∠CON
=∠MON-![]() ∠AOB-
∠AOB-![]() ∠COD=∠MON-
∠COD=∠MON-![]() (∠AOB+∠COD)
(∠AOB+∠COD)
=∠MON-![]() (∠AOD-∠BOC)
(∠AOD-∠BOC)
=β-![]() (α-∠BOC)
(α-∠BOC)
=β-![]() α+
α+![]() ∠BOC,
∠BOC,
∴∠BOC=2β-α.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案