题目内容
【题目】如图,二次函数y=x2+bx+c的图象交x轴于A(﹣1,0)、B(3,0)两点,交y轴于点C,连接BC,动点P以每秒1个单位长度的速度从A向B运动,动点Q以每秒 ![]() 个单位长度的速度从B向C运动,P、Q同时出发,连接PQ,当点Q到达C点时,P、Q同时停止运动,设运动时间为t秒.
个单位长度的速度从B向C运动,P、Q同时出发,连接PQ,当点Q到达C点时,P、Q同时停止运动,设运动时间为t秒.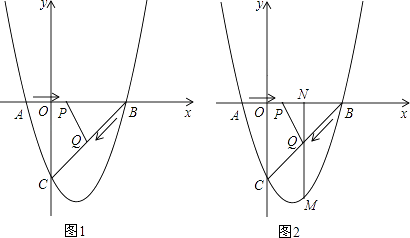
(1)求二次函数的解析式;
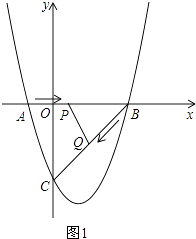
(2)如图1,当△BPQ为直角三角形时,求t的值;
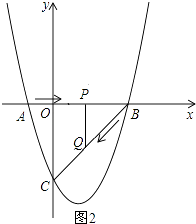
(3)如图2,过点Q作QN⊥x轴于N,交抛物线于点M,连结MC,MB,当t为何值时,△MCB的面积最大,并求出此时点M的坐标和△MCB面积的最大值.
【答案】
(1)
解:∵二次函数y=x2+bx+c的图象交x轴于A(﹣1,0)、B(3,0)两点,
∴抛物线的解析式为y=(x+1)(x﹣3),整理得:y=x2﹣2x﹣3.
(2)
解:∵当x=0时,y=﹣3,
∴C(0,﹣3).
∴OB=OC.
∴∠PBQ=45°.
如图1所示:当∠PQB=90°时.则PB= ![]() BQ.
BQ.
∵AP=t,BQ= ![]() t,AB=4,
t,AB=4,
∴AP+PB=t+2t=4.
∴t= ![]() .
.
如图2所示:当∠QPB=90°时.
∵∠PBQ=45°,∠BPQ=90°,
∴PB= ![]() BQ=
BQ= ![]() ×
× ![]() t=t.
t=t.
∵AP=t,AB=4,
∴t+t=4.
解得:t=2.
综上所述,当t=2或t= ![]() 时,△BPQ为直角三角形.
时,△BPQ为直角三角形.
(3)
解:设直线BC的解析式为y=kx+b.
∵将C(0,﹣3)、B(3,0)代入得: ![]() ,解得:k=1,b=﹣3,
,解得:k=1,b=﹣3,
∴直线BC的解析式为y=x﹣3.
设M(a,a2﹣2a﹣3),则Q(a,a﹣3).则QM=a﹣3﹣(a2﹣2a﹣3)=﹣a2+3a.
∵S△BCM= ![]() OBQM=
OBQM= ![]() ×3(﹣a2+3a)=﹣
×3(﹣a2+3a)=﹣ ![]() (a2﹣3a)=﹣
(a2﹣3a)=﹣ ![]() (a﹣
(a﹣ ![]() )2+
)2+ ![]() ,
,
∴当a= ![]() 时,△BCM的面积的最大值为
时,△BCM的面积的最大值为 ![]() .
.
∴点P的坐标( ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)由题意可知a=1,依据二次函数的交点式可知抛物线的解析式为y=(x+1)(x﹣3),然后整理即可;(2)分为∠PQB=90°和∠BPQ=90°两种情况求解.当∠PQB=90°时,PB= ![]() QB=2t,然后依据AB=AP+PB列方程求解即可;当∠BPQ=90°时,PB=
QB=2t,然后依据AB=AP+PB列方程求解即可;当∠BPQ=90°时,PB= ![]() QB=t,然后依据AB=AP+PB列方程求解即可;(3)先求得直线BC的解析式,然后设M(a,a2﹣2a﹣3),则Q(a,a﹣3).则QM=﹣a2+3a.由S△BCM
QB=t,然后依据AB=AP+PB列方程求解即可;(3)先求得直线BC的解析式,然后设M(a,a2﹣2a﹣3),则Q(a,a﹣3).则QM=﹣a2+3a.由S△BCM![]() OBQM,得到△BCN的面积与a的函数关系式,然后依据配方法可求得△BCN的面积的最大值以及点P的坐标.
OBQM,得到△BCN的面积与a的函数关系式,然后依据配方法可求得△BCN的面积的最大值以及点P的坐标.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 阅读快车系列答案
阅读快车系列答案【题目】在弹性限度内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表,下列说法不正确的是( )
x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 20 | 20.5 | 21 | 21.5 | 22 | 22.5 |
A. x与y都是变量,且x是自变量,y是x的函数
B. 弹簧不挂重物时的长度为0 cm
C. 物体质量每增加1 kg,弹簧长度y增加0.5 cm
D. 所挂物体质量为7 kg时,弹簧长度为23.5 cm