��Ŀ����
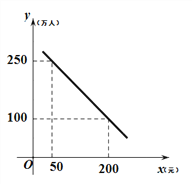
����Ŀ����һ��ֱ�Ĺ�·����M��N���أ��׳���M��ʻ��N�أ��ٶ�Ϊ60km/h���ҳ���M��ʻ��N�أ��ٶ�Ϊ40km/h��������N��ʻ��M�أ��ٶ�Ϊ80km/h��������ͬʱ�������ȵ�Ŀ�ĵصij�ֹͣ������;�м׳��������ϣ�����ͣ��������2.5h���ú�������ԭ��ʻ��N�أ���׳���ʻ��ʱ��Ϊt��h�����ס�������֮��ľ���ΪS1��km�����ס���������M�صľ���ΪS2��km����S1��t֮��Ĺ�ϵ��ͼ1��ʾ��S2��t֮��Ĺ�ϵ��ͼ2��ʾ���������е���Ϣ�ش��������⣺

��1����ͼ1�е�C��ʵ���������� ����
�ڵ�B�ĺ��������� ������E�ĺ��������� ������Q���������� ����
��2�������ͼ2���߶�QR����ʾ��S2��t֮��Ĺ�ϵʽ��
��3�����ס���������70kmʱ����ֱ��д��t��ֵ��
���𰸡���1���پ���3Сʱ������������������1��3.75����3.5��60������2��y��60x��150����3��![]() ��4Сʱ
��4Сʱ
��������
��1���ٸ��������֪��C��ʵ�������Ǿ���3Сʱ���������������������������ʱ������ʻ��ʱ�䣬�����B���꣬�������D����Q���꣬��ͼ������E���꣬������⣻
��2���ô���ϵ�����������ʽ��
��3���ɼס���������70km������������г����̿���⣮
�⣺��1���١ߵ�C�����꣨3��0����
���CC��ʵ�������Ǿ���3Сʱ����������������
�ʴ�Ϊ������3Сʱ����������������
�������ʻxСʱ�׳��������ϣ�
������ɵ�60x+80��3��300
��x��1��
���B�ĺ�����Ϊ1��
���D�ĺ�����Ϊ3.5��
���Q������3.5��60��
��ͼ���֪����E��ʾ��������N�أ�
��t��![]() ��3.75h��
��3.75h��
���E�ĺ�����Ϊ3.75��
�ʴ�Ϊ��1��3.75����3.5��60��
��2�����߶�QR�ĺ�������ʽΪ��y��kx+b��
![]()
��ã�![]()
���߶�QR�ĺ�������ʽΪ��y��60x��150��
��3���辭��xСʱ���ס���������70km��
������ɵã�40x��60��70��40x��60��x��2.5����70
��x��![]() ��4��
��4��
��![]() ��4Сʱ���ס���������70km��
��4Сʱ���ס���������70km��