题目内容
【题目】如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠ACB=74°,∠ABC=46°,且∠BAD+∠CAD=180°,那么∠BDC的度数为_____.
【答案】30°
【解析】
延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,根据BD是∠ABC的平分线可得出△BDE≌△BDF,故DE=DF,过D点作DG⊥AC于G点,可得出△ADE≌△ADG,△CDG≌△CDF,进而得出CD为∠ACF的平分线,得出∠DCA=53°,再根据三角形内角和定理即可得出结论.
解:
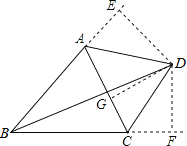
延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,
∵BD是∠ABC的平分线
在△BDE与△BDF中,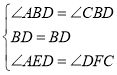 ,
,
∴△BDE≌△BDF(ASA),
∴DE=DF,
又∵∠BAD+∠CAD=180°
∠BAD+∠EAD=180°
∴∠CAD=∠EAD,
∴AD为∠EAC的平分线,
过D点作DG⊥AC于G点,
在Rt△ADE与Rt△ADG中,![]() ,
,
∴△ADE≌△ADG(HL),
∴DE=DG,
∴DG=DF.
在Rt△CDG与Rt△CDF中,![]() ,
,
∴Rt△CDG≌Rt△CDF(HL),
∴CD为∠ACF的平分线,
∠ACB=74°,
∴∠DCA=53°,
∴∠BDC=180°﹣∠CBD﹣∠DCA﹣∠ACB=180°﹣23°﹣53°﹣74°=30°.
故答案为:30°

练习册系列答案
相关题目