题目内容
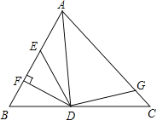
【题目】如图，在△ABC中，DF∥AB，DE∥BC，连接BD．
（1）求证：△DEB≌△BFD；
（2）若点D是AC边的中点，当△ABC满足条件_____时，四边形DEBF为菱形．
【答案】AB=BC
【解析】（1）根据ASA证明△DEB≌△BFD即可；
（2）根据菱形的判定解答即可．
（1）∵DF∥AB，DE∥BC，∴∠EDB=∠FBD，∠EBD=∠FDB．在△DEB与△BFD中，∵
，∴△DEB≌△BFD（ASA）；
（2）当△ABC满足AB=BC时，四边形DEBF为菱形，理由如下：
∵DF∥AB，DE∥BC，∴四边形DEBF为平行四边形．
∵DE∥BC，DF∥AB，点D是AC边的中点，∴BC=2DE，AB=2DF．
∵AB=BC，∴DE=DF，∴平行四边形DEBF是菱形．
故答案为：AB=BC．
练习册系列答案
相关题目
