题目内容
 如图,△ABC、△DEF都是等边三角形,点D为AB的中点,E在BC上运动,DF和EF分别交AC于G、H两点,BC=2,问E在何处时CH的长度最大?
如图,△ABC、△DEF都是等边三角形,点D为AB的中点,E在BC上运动,DF和EF分别交AC于G、H两点,BC=2,问E在何处时CH的长度最大?
解:设EC=x,CH=y,则BE=2-x,
∵△ABC、△DEF都是等边三角形,
∴∠B=∠DEF=60°,
∵∠B+∠BDE=∠DEF+∠HEC,
∴∠BDE=∠HEC,
∴△BED∽△CHE,
∴ ,
,
∵AB=BC=2,点D为AB的中点,
∴BD=1,
∴ ,
,
即:y=-x2+2x=-(x-1)2+1.
∴当x=1时,y最大.此时,E在BC中点.
分析:首先设EC=x,CH=y,则BE=2-x,由△ABC、△DEF都是等边三角形,易得△BED∽△CHE,根据相似三角形的对应边成比例,即可得 ,又由点D为AB的中点,AB=BC=2,代入比例式,即可求得y=-x2+2x=-(x-1)2+1,然后根据二次函数的性质,即可求得答案.
,又由点D为AB的中点,AB=BC=2,代入比例式,即可求得y=-x2+2x=-(x-1)2+1,然后根据二次函数的性质,即可求得答案.
点评:此题考查了相似三角形的判定与性质、等边三角形的性质以及二次函数的性质.此题难度适中,解题的关键是证得△BED∽△CHE,注意数形结合思想与方程思想的应用.
∵△ABC、△DEF都是等边三角形,
∴∠B=∠DEF=60°,
∵∠B+∠BDE=∠DEF+∠HEC,
∴∠BDE=∠HEC,
∴△BED∽△CHE,
∴
 ,
,∵AB=BC=2,点D为AB的中点,
∴BD=1,
∴
 ,
,即:y=-x2+2x=-(x-1)2+1.
∴当x=1时,y最大.此时,E在BC中点.
分析:首先设EC=x,CH=y,则BE=2-x,由△ABC、△DEF都是等边三角形,易得△BED∽△CHE,根据相似三角形的对应边成比例,即可得
 ,又由点D为AB的中点,AB=BC=2,代入比例式,即可求得y=-x2+2x=-(x-1)2+1,然后根据二次函数的性质,即可求得答案.
,又由点D为AB的中点,AB=BC=2,代入比例式,即可求得y=-x2+2x=-(x-1)2+1,然后根据二次函数的性质,即可求得答案.点评:此题考查了相似三角形的判定与性质、等边三角形的性质以及二次函数的性质.此题难度适中,解题的关键是证得△BED∽△CHE,注意数形结合思想与方程思想的应用.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
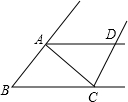 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
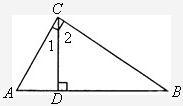
 ,且CB=CE.
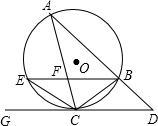
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.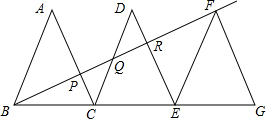 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且