题目内容
如图,△ABC内接于⊙O,AB的延长线与过C点的切线GC相交于点D,BE与AC相交于点F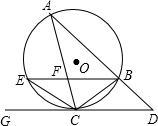 ,且CB=CE.
,且CB=CE.求证:(1)BE∥DG;
(2)CB2-CF2=BF•FE.
分析:(1)欲证BE∥DG,需证得两直线的同位角或内错角相等,由等腰三角形的性质,易得∠CEB=∠CBE,由弦切角定理,得∠BCD=∠CEB,将等角代换后可证得两直线平行;
(2)先将所求的等式进行适当变形,由相交弦定理,得BF•FE=AF•FC,因此所求的结论可化为CB2-CF2=AF•FC,化简得:CB2=CF•AC,因此只需证明△CBF∽△CAB即可.
(2)先将所求的等式进行适当变形,由相交弦定理,得BF•FE=AF•FC,因此所求的结论可化为CB2-CF2=AF•FC,化简得:CB2=CF•AC,因此只需证明△CBF∽△CAB即可.
解答:证明:(1)∵CB=CE,
∴∠E=∠CBE.
∵CG为⊙O切线,
∴∠BCD=∠E.
∴∠CBE=∠BCD.
∴BE∥DG.
(2)∵∠A=∠E,
∴∠A=∠CBE.
∵∠ACB=∠ACB,
∴△CBF∽△CAB,
=
.
∴CB2=CF•AC=CF•(CF+AF)=CF2+CF•AF.
即CB2-CF2=AF•CF.
由相交弦定理,得AF•CF=BF•FE.
∴CB2-CF2=BF•FE.
∴∠E=∠CBE.
∵CG为⊙O切线,
∴∠BCD=∠E.
∴∠CBE=∠BCD.
∴BE∥DG.
(2)∵∠A=∠E,
∴∠A=∠CBE.
∵∠ACB=∠ACB,
∴△CBF∽△CAB,
| CB |
| CF |
| AC |
| CB |
∴CB2=CF•AC=CF•(CF+AF)=CF2+CF•AF.
即CB2-CF2=AF•CF.
由相交弦定理,得AF•CF=BF•FE.
∴CB2-CF2=BF•FE.
点评:本题考查了平行线的判断、相似三角形的性质及圆周角定理、等腰三角形的性质等知识.

练习册系列答案
相关题目
 15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD=
15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD= 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.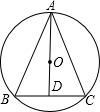 已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积.
已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积. 18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( )
18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( ) 如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.
如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.