题目内容
 如图,在等腰直角△ABC中,∠ABC=90°,AB=BC,AD∥BC,E是AB的中点,BE=AD.
如图,在等腰直角△ABC中,∠ABC=90°,AB=BC,AD∥BC,E是AB的中点,BE=AD.(1)试说明:CE⊥BD;
(2)线段AC与ED之间存在什么关系?为什么?
(3)判断△BDC的形状,并说明理由.
分析:(1)利用全等的性质∠ABD=∠BCE,然后利用等价变换的知识可得出∠BFC=90°,从而即可得出答案.
(2)根据AC垂直平分DE,E是AB中点及AD∥BC可得出AC与ED之间存在的关系.
(3)根据等腰三角形及中垂线的性质即可作出判断.
(2)根据AC垂直平分DE,E是AB中点及AD∥BC可得出AC与ED之间存在的关系.
(3)根据等腰三角形及中垂线的性质即可作出判断.
解答: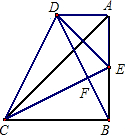 解:(1)∵等腰直角△ABC,∠ABC=90°
解:(1)∵等腰直角△ABC,∠ABC=90°
∴AB=BC,∠ACB=∠CAB=45°
∵AD∥BC
∴∠DAB+∠ABC=180°∴∠DAB=90°
∴∠DAB=∠ABC=90°
在△ABD和△BCE中,
∴△ABD≌△BCE(SAS)
∴∠ABD=∠BCE,
∵∠ABC=90°
∴∠ABD+∠CBD=90°
∴∠BCE+∠CBD=90°
∵△BCF中,∠BFC+∠FBC+∠BCF=180°
∴∠BFC=90°,
∴CE⊥BD.
(2)AC垂直平分DE,
∵E是AB中点,
∴AE=BE,
∵BE=AD,
∴AD=AE,
∵AD∥BC,
∴∠DAC=∠ACB=45°,
∴∠DAC=∠CAE=45°,
∵AD=AE,∠DAC=∠CAE,
∴AC垂直平分DE.
(3)△BDC是等腰三角形,
∵AC垂直平分DE,
∴CD=CE,
∵△ABD≌△BCE,
∴BD=CE,
∴BD=CD,
∴△BCD是等腰三角形.
 解:(1)∵等腰直角△ABC,∠ABC=90°
解:(1)∵等腰直角△ABC,∠ABC=90°∴AB=BC,∠ACB=∠CAB=45°
∵AD∥BC
∴∠DAB+∠ABC=180°∴∠DAB=90°
∴∠DAB=∠ABC=90°
在△ABD和△BCE中,
|
∴△ABD≌△BCE(SAS)
∴∠ABD=∠BCE,
∵∠ABC=90°
∴∠ABD+∠CBD=90°
∴∠BCE+∠CBD=90°
∵△BCF中,∠BFC+∠FBC+∠BCF=180°
∴∠BFC=90°,
∴CE⊥BD.
(2)AC垂直平分DE,
∵E是AB中点,
∴AE=BE,
∵BE=AD,
∴AD=AE,
∵AD∥BC,
∴∠DAC=∠ACB=45°,
∴∠DAC=∠CAE=45°,
∵AD=AE,∠DAC=∠CAE,
∴AC垂直平分DE.
(3)△BDC是等腰三角形,
∵AC垂直平分DE,
∴CD=CE,
∵△ABD≌△BCE,
∴BD=CE,
∴BD=CD,
∴△BCD是等腰三角形.
点评:本题考查等腰三角形的性质及中垂线的性质,难度较大,注意熟练掌握一些基本性质,这是解答此类综合题得基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
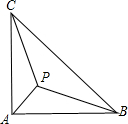 如图,在等腰直角三角形ABC中,∠A=90°,P是△ABC内一点,PA=1,PB=3,PC=
如图,在等腰直角三角形ABC中,∠A=90°,P是△ABC内一点,PA=1,PB=3,PC= 23、如图,在等腰直角三角形ABC和DEC中,∠BCA=∠BCE=90°,点E在边AB上,ED与AC交于点F,连接AD.
23、如图,在等腰直角三角形ABC和DEC中,∠BCA=∠BCE=90°,点E在边AB上,ED与AC交于点F,连接AD.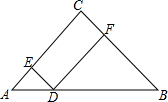 (2013•海沧区一模)如图,在等腰直角三角形ABC中,AC=BC=2,D为AB上的动点(不与A,B重合),过D作DE⊥AC于E,DF⊥BC于F,设AD的长度为x,DE与DF的长度和为y.则能表示y与x之间的函数关系的图象大致是( )
(2013•海沧区一模)如图,在等腰直角三角形ABC中,AC=BC=2,D为AB上的动点(不与A,B重合),过D作DE⊥AC于E,DF⊥BC于F,设AD的长度为x,DE与DF的长度和为y.则能表示y与x之间的函数关系的图象大致是( ) 如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.
如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.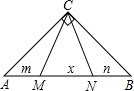 如图,在等腰直角△ABC的斜边AB上取两点M、N(不与A、B重合)使∠MCN=45°,记AM=m,MN=x,NB=n,试判断以x、m、n为边长的三角形的形状,并给予说明.
如图,在等腰直角△ABC的斜边AB上取两点M、N(不与A、B重合)使∠MCN=45°,记AM=m,MN=x,NB=n,试判断以x、m、n为边长的三角形的形状,并给予说明.