题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点
两点![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与
与![]() 关于抛物线的对称轴对称.
关于抛物线的对称轴对称.
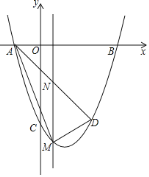
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线上的一点,当
是抛物线上的一点,当![]() 的面积是8,求出点
的面积是8,求出点![]() 的坐标;
的坐标;
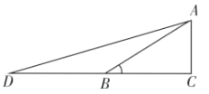
(3)过直线![]() 下方的抛物线上一点
下方的抛物线上一点![]() 作
作![]() 轴的平行线,与直线
轴的平行线,与直线![]() 交于点
交于点![]() ,已知
,已知![]() 点的横坐标是
点的横坐标是![]() ,试用含
,试用含![]() 的式子表示
的式子表示![]() 的长及△ADM的面积
的长及△ADM的面积![]() ,并求当
,并求当![]() 的长最大时
的长最大时![]() 的值.
的值.
【答案】【解析】(1)y=(x-1)2-4, 点D的坐标为(2,-3);(2)点P的坐标为![]() 或
或![]() 或(1,-4);(3)当
或(1,-4);(3)当![]()
![]() ,
,![]() ,当MN的长最大时S的值为
,当MN的长最大时S的值为![]() .
.
【解析】
(1)根据点C的坐标,利用二次函数图象上点的坐标特征可求出n值,进而可得出抛物线的解析式,由抛物线的解析式利用二次函数的性质可得出抛物线的对称轴,结合点C的坐标可得出点D的坐标;
(2)利用二次函数图象上点的坐标特征可求出点A,B的坐标及AB的长,设点P的坐标为(a,b),由三角形的面积公式结合△ABP的面积是8,可求出b值,再利用二次函数图象上点的坐标特征可求出点P的坐标;
(3)根据点A,D的坐标利用待定系数法可求出直线AD的解析式,由点M的横坐标为m可得出点M,N的坐标,进而可得出MN的长,结合S=S△AMN+S△DMN可用含m的式子表示△ADM的面积S,再利用二次函数的性质即可解决最值问题.
解:(1)把C(0,-3)代入y=(x-1)2+n,得,-3=(0-1)2+n,
解得n=-4,∴抛物线的解析式为y=(x-1)2-4,
∴抛物线的对称轴为直线x=1∵点D与点C关于抛物线的对称轴对称,
∴点D的坐标为(2,-3).
(2)当y=0时,(x-1)2-4=0,
解得:x1=-1,x2=3,
∴点A的坐标为(-1,0),点B的坐标为(3,0),AB=3-(-1)=4.
设点P的坐标为(a,b),
∵△ABP的面积是8,
∴![]() AB|b|=8,即
AB|b|=8,即![]()
×4|b|=8,
∴b=±4.
当b=4时,(a-1)2-4=4,解得:a1=1-2![]() ,a2=1+2
,a2=1+2![]() ,
,
∴点P的坐标为(1-2![]() ,4)或(1+2
,4)或(1+2![]() ,4);
,4);
当b=-4时,(a-1)2-4=-4,解得:a3=a4=1,
∴点P的坐标为(1,-4).
∴当△ABP的面积是8,点P的坐标为(1-2![]() ,4)或(1+2
,4)或(1+2![]() ,4)或(1,-4).
,4)或(1,-4).
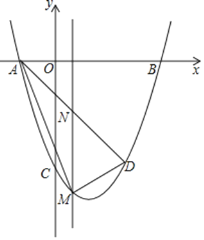
(3)设直线AD的解析式为y=kx+c(k≠0),
将A(-1,0),D(2,-3)代入y=kx+c,得:
![]() ,
,
解得:![]() ,
,
∴直线AD的解析式为y=-x-1.
∵点M的横坐标是m(-1<m<2),
∴点M的坐标为(m,(m-1)2-4),点N的坐标为(m,-m-1),
∴MN=-m-1-[(m-1)2-4]=-m2+m+2(-1<m<2),S=S△AMN+S△DMN=![]() MN(m+1)+
MN(m+1)+![]() MN(2-m)=
MN(2-m)=![]() mn=-
mn=-![]() m2+
m2+![]() m+3(-1<m<2).
m+3(-1<m<2).
∵MN=-m2+m+2=-(m-![]() )2+
)2+![]() ,-1<0,
,-1<0,
∴当m=![]() 时,MN取得最大值,最大值为
时,MN取得最大值,最大值为![]() ,此时S的值为
,此时S的值为![]() ×
×![]() =
=![]() ,
,
∴当MN的长最大时S的值为![]() .
.

 阅读快车系列答案
阅读快车系列答案