��Ŀ����
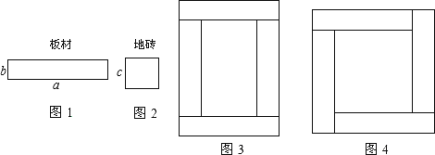
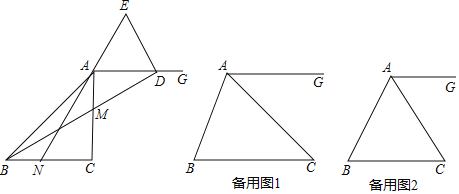
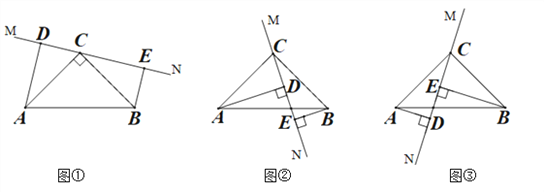
����Ŀ����֪Rt��ABC�У���ACB=90������D��E�ֱ���BC��AC���ϣ�����BE��AD���ڵ�P����AC=kBD��CD=kAE��kΪ��������̽����APE�Ķ�����
��1����ͼ1����k=1�����APE�Ķ���Ϊ ��
��2����ͼ2����k=![]() �����ʣ�1���еĽ����Ƿ����������������˵�����ɣ����������������APE�Ķ�����
�����ʣ�1���еĽ����Ƿ����������������˵�����ɣ����������������APE�Ķ�����
��3����ͼ3����k=![]() ����D��E�ֱ���CB��CA���ӳ����ϣ���2���еĽ����Ƿ��������˵�����ɣ�
����D��E�ֱ���CB��CA���ӳ����ϣ���2���еĽ����Ƿ��������˵�����ɣ�
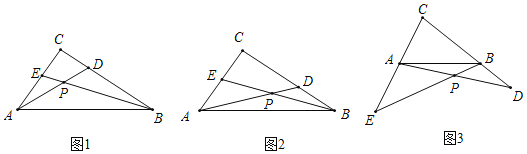
���𰸡���1��45�㣻��2����1���н��۲����������ɼ���������3����2���н��۳��������ɼ�����.
����������1�����жϳ��ı���ADBF��ƽ���ı��Σ��ó�BD=AF��BF=AD�������жϳ���FAE�ա�ACD���ó�EF=AD=BF�����жϳ���EFB=90�㣬���ɵó����ۣ�
��2�����жϳ��ı���ADBF��ƽ���ı��Σ��ó�BD=AF��BF=AD�������жϳ���FAE�ס�ACD�����жϳ���EFB=90�㣬���ɵó����ۣ�
��3�����жϳ��ı���ADBF��ƽ���ı��Σ��ó�BD=AF��BF=AD�������жϳ���ACD�ס�HEA�����жϳ���EFB=90�㣬���ɵó����ۣ�
��1����ͼ1������A��AF��CB������B��BF��AD�ཻ��F������EF��
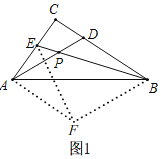
���FBE=��APE����FAC=��C=90�����ı���ADBF��ƽ���ı��Σ�
��BD=AF��BF=AD��
��AC=BD��CD=AE��
��AF=AC��
�ߡ�FAC=��C=90����
����FAE�ա�ACD��
��EF=AD=BF����FEA=��ADC��
�ߡ�ADC+��CAD=90����
���FEA+��CAD=90��=��EHD��
��AD��BF��
���EFB=90����
��EF=BF��
���FBE=45����
���APE=45����
��2����1���н��۲��������������£�
��ͼ2������A��AF��CB������B��BF��AD�ཻ��F������EF��
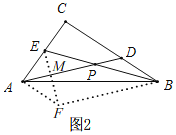
���FBE=��APE����FAC=��C=90�����ı���ADBF��ƽ���ı��Σ�
��BD=AF��BF=AD��
��AC=![]() BD��CD=
BD��CD=![]() AE��
AE��
��![]() ��
��
��BD=AF��
��![]() ��
��
�ߡ�FAC=��C=90����
����FAE�ס�ACD��
��![]() ����FEA=��ADC��
����FEA=��ADC��
�ߡ�ADC+��CAD=90����
���FEA+��CAD=90��=��EMD��
��AD��BF��
���EFB=90����
��Rt��EFB��tan��FBE=![]() ��
��
���FBE=30����
���APE=30����
��3����2���н��۳�������ͼ3����EH��CD��DH��BE��EH��DH�ཻ��H������AH��
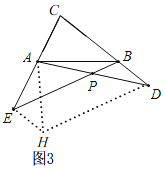
���APE=��ADH����HEC=��C=90�����ı���EBDH��ƽ���ı��Σ�
��BE=DH��EH=BD��
��AC=![]() BD��CD=
BD��CD=![]() AE��
AE��
��![]() ��
��
�ߡ�HEA=��C=90����
����ACD�ס�HEA��
��![]() ����ADC=��HAE��
����ADC=��HAE��
�ߡ�CAD+��ADC=90����
���HAE+��CAD=90����
���HAD=90����
��Rt��DAH��tan��ADH=![]() ��
��
���ADH=30����
���APE=30����

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�����Ŀ������ʦԪ�����ڼ䵽������Բ�̳�����һ̨ijƷ�ƱʼDZ����ԣ�ǡ���̳����Ƴ���ӭԪ�����������ۻ�������Ż���������
�����ܽ�ԭ�ۣ� | �ۿ� |
������5000Ԫ�IJ��� | ���� |
����5000Ԫ�Ҳ�����10000Ԫ�IJ��� | ���� |
����10000Ԫ�Ҳ�����20000Ԫ�IJ��� | ���� |
���� | ���� |
���磺���������Ʒԭ��Ϊ15000Ԫ��ʵ�ʸ�����Ϊ��
5000��90%+��10000��5000����80%+��15000��10000����70%��12000Ԫ��
��1��������Ʒ�Ƶ��Ե�ԭ��Ϊ8000Ԫ/̨�����������ʦʵ�ʸ����
��2����֪����ʦ����һ̨��Ʒ�Ƶ���ʵ�ʸ���5700Ԫ��
�����Ʒ�Ƶ��Ե�ԭ���Ƕ���Ԫ/̨��
�����۳���̨�����̳��Կɻ���14%��������Ʒ�Ƶ��ԵĽ���Ϊ����Ԫ/̨��