题目内容
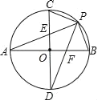
【题目】如图,直径AB、CD相互垂直,P为弧BC上任意一点,连PC、PA、PD、PB,下列结论:①∠APC=∠DPE;②∠AED=∠DFA;③![]() ;其中正确的是( )
;其中正确的是( )
A. ①③B. 只有①C. 只有②D. ①②③
【答案】A
【解析】
①利用垂径定理,可得![]() ,又由圆周角定理,即可证得∠APC=∠DPE;
,又由圆周角定理,即可证得∠APC=∠DPE;
②由于∠A不一定等于∠D,故∠AED=∠DFA错误;
③连AC,AD,BD,将△ACP绕A点顺时针旋转90°,使AC与AD重合(由AB⊥CD知AC=AD)点P旋转到Q点,可证得△APQ是等腰直角三角形,CP+DP=![]() AP,同理可得BP+AP=
AP,同理可得BP+AP=![]() DP,继而可证得结论.
DP,继而可证得结论.
解:∵直径AB、CD相互垂直,
∴![]() ,
,
∴∠APC=∠DPE;
故①正确;
∵∠AED=∠DPE+∠D,∠DFA=∠APF+∠A,
∵P为![]() 上任意一点,
上任意一点,
∴∠A不一定等于∠D,
∴∠AED不一定等于∠DFA;
故②错误;
连AC,AD,BD,将△ACP绕A点顺时针旋转90°,使AC与AD重合(由AB⊥CD知AC=AD)点P旋转到Q点,
∴AQ=AP,CP=QD,
∵∠PAQ=90°,AQ=AP,
∵∠ADQ+∠ADP=∠ACP+∠ADP=180°,
∴P,D,Q三点共线,
∴∠Q=∠APD=45°,
∴PQ2=PA2+AQ2,
∴PQ=![]() AP,
AP,
即CP+DP=![]() AP,
AP,
同理:BP+AP=![]() DP,
DP,
∴![]() .
.
故③正确.
故选:A.


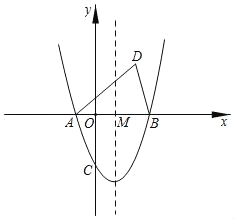
【题目】1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都匀速上升了50min.设气球上升时间为x(x≥0).
(Ⅰ)根据题意,填写下表
上升时间/min | 10 | 30 | … | x |
1号探测气球所在位置的海拔/m | 15 | … | ||
2号探测气球所在位置的海拔/m | 30 | … |
(Ⅱ)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由.
(Ⅲ)当0≤x≤50时,两个气球所在位置的海拔最多相差多少米?
【题目】随着生活水平的提高,人们对空气质量的要求也越来越高。为了了解![]() 月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区
月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区![]() 年
年![]() 月
月![]() 日——
日——![]() 年
年![]() 月
月![]() 日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
收集数据
朝阳区 |
|
|
|
|
|
|
|
|
|
|
南关区 |
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按下表整理、描述这两城区空气质量指数的数据.
空气质量 | 优 | 良 | 轻微污染 | 中度污染 | 重度污染 |
朝阳区 | |||||
南关区 |
|
|
|
|
|
(说明:空气质量指数![]() 时,空气质量为优;
时,空气质量为优;![]() 空气质量指数
空气质量指数![]() 时,空气质量为良;
时,空气质量为良;![]() 空气质量指数
空气质量指数![]() 时,空气质量为轻微污染;
时,空气质量为轻微污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为中度污染;
时,空气质量为中度污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为重度污染.)
时,空气质量为重度污染.)
分析数据
两城区的空气质量指数的平均数、中位数、方差如下表所示.
城区 | 平均数 | 中位数 | 方差 |
朝阳区 |
|
|
|
南关区 |
|
|
请将以上两个表格补充完整.
得出结论可以推断出哪个城区这十天中空气质量情况比较好?请至少从两个不同的角度说明推断的合理性.