题目内容
【题目】一艘轮船和一艘快艇沿相同的路线从甲港出发驶向乙港的过程中,路程![]() 随时间
随时间![]() 变化的图像如图示(分别是正比例函数的图像和一次函数的图像).根据图中提供的信息解答下列问题:
变化的图像如图示(分别是正比例函数的图像和一次函数的图像).根据图中提供的信息解答下列问题:
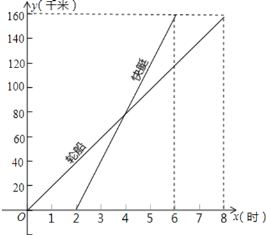
(1)分别求出表示轮船和快艇行驶过程中路程![]() 和时间
和时间![]() 之间的函数解析式(不要求写出自变量的取值范围);
之间的函数解析式(不要求写出自变量的取值范围);
(2)轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少?
(3)快艇出发多长时间赶上轮船?
【答案】(1)轮船行驶过程的函数式为y=20x.;快艇行驶过程的函数解析式为y=40x80;(2)轮船在途中的行驶速度为20(千米/时);快艇在途中行驶的速度为40(千米/时);(3)快艇出发2小时后赶上轮船.
【解析】
(1)可根据图中给出的信息,用待定系数法分别求出轮船与快艇的函数关系式.
(2)可根据轮船与快艇到乙港时用的时间和走的路程,根据速度=路程÷时间,求出速度是多少.
(3)当快艇追上轮船时两者走的路程相同,根据(1)求出的函数式,让两者的路程相等,即可得出时间的值.
(1)设表示轮船行驶过程的函数式为y=kx.由图象知:
当x=8时,y=160.
∴8k=160,解得:k=20
∴表示轮船行驶过程的函数式为y=20x.
设表示快艇行驶过程的函数解析式为y=ax+b.
由图象知:当x=2时,y=0;当x=6时,y=160
∴![]() ,
,
解得![]()
因此表示快艇行驶过程的函数解析式为y=40x80;
(2)由图象可知,轮船在8小时内行驶了160千米。快艇在4小时内行驶了160千米。
故轮船在途中的行驶速度为160÷8=20(千米/时)
快艇在途中行驶的速度为160÷4=40(千米/时);
(3)设轮船出发x小时后快艇追上轮船。
20x=40x80,
x=4,
则x2=2.
答:快艇出发2小时后赶上轮船.

练习册系列答案
相关题目