Question

【题目】在平行四边形ABCD中，点E、F分别在边AB、BC上，DE、AF交于点M．

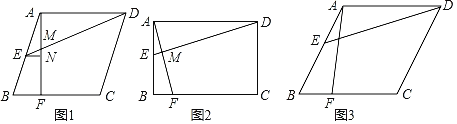
（1）如图1，E为AB的中点，AF⊥BC交BC于点F，过点E作EN⊥AF交AF于点N，，直接写出的值是　 　；

（2）如图2，∠B＝90°，∠ADE＝∠BAF，求证：△AEM∽△AFB；

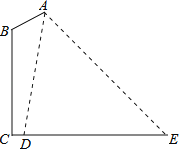
（3）如图3，∠B＝60°，AB＝AD，∠ADE＝∠BAF，求证：．

Answer 1

【答案】（1）；（2）详见解析；（3）详见解析．

【解析】

（1）证明EN∥BF，得出；

（2）证明四边形ABCD是矩形，得出∠BAD＝∠ABC＝90°，则∠AED＝∠AFB，可得出结论；

（3）连接AC，过点B作BP∥AC交AF的延长线于点P，证明△BFP∽△CFA，得出，证明△ADE≌△BAP（ASA），得出AE＝BP，则可得出结论．

解：（1）∵EN⊥AF，BF⊥AF，

∴EN∥BF，

又∵E为AB的中点，

∴BF＝2EN，

∵，

∴，

∴，

故答案为：；

（2）证明：∵四边形ABCD是平行四边形，∠ABC＝90°，

∴四边形ABCD是矩形，

∴∠BAD＝∠ABC＝90°，

∵∠ADE＝∠BAF，

∴∠BAD﹣∠BAF＝∠ABC﹣∠BAF

∴∠AED＝∠AFB，

又∵∠BAF＝∠MAE，

∴△AEM∽△AFB；

（3）证明：如图，连接AC，过点B作BP∥AC交AF的延长线于点P，

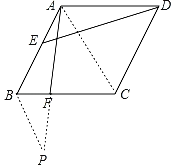
∴△BFP∽△CFA，

∴，

∵四边形ABCD是平行四边形，AB＝AD，

∴四边形ABCD是菱形，

∵∠ABC＝60°，

∴∠PBC＝∠ACB＝60°，

∴∠ABP＝120°，

∴∠DAE＝∠ABP，

在△ADE与△BAP中，

，

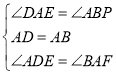∴△ADE≌△BAP（ASA），

∴AE＝BP，

又∵AC＝AD，

∴．