题目内容

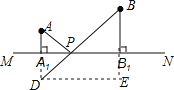
【题目】如图,直线MN表示一条铁路,A,B是两个城市,它们到铁路的垂直距离分别为AA1=20km,BB1=40km,已知A1B1=80km,现要在A1,B1之间设一个中转站P，使两个城市到中转站的距离之和最短，请你设计一种方案确定P点的位置，并求这个最短距离.

【答案】设计见解析，最短距离为100km

【解析】

利用轴对称求最短路径的方法得至点P的位置，再根据勾股定理求得最短距离．

如图所示，延长AA1到D使A1D=AA1，连接BD交MN于点P，则点P即为所求,则PA+PB的最小距离即为BD的长度.

过D作DE⊥BB1交BB1于E，
∵AA1=20km，BB1=40km，A1B1=80km，
∴DE= A1B1=80km，BE= BB1+ AA1=60km，
∴BD==100km，即PA+PB的最小距离为100km．

练习册系列答案
相关题目

【题目】如图，在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．

（1）求证：ED为⊙O的切线；

（2）如果⊙O的半径为，ED=2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．

【答案】（1）证明见解析；（2）

【解析】试题分析：（1）首先连接OD，由OE∥AB，根据平行线与等腰三角形的性质，易证得≌ 即可得，则可证得为的切线；
（2）连接CD，根据直径所对的圆周角是直角，即可得 利用勾股定理即可求得的长，又由OE∥AB，证得根据相似三角形的对应边成比例，即可求得的长，然后利用三角函数的知识，求得与的长，然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案．

试题解析：(1)证明：连接OD，

∵OE∥AB，

∴∠COE=∠CAD，∠EOD=∠ODA，

∵OA=OD,

∴∠OAD=∠ODA，

∴∠COE=∠DOE，

在△COE和△DOE中，

∴△COE≌△DOE(SAS)，

∴ED⊥OD，

∴ED是的切线；

(2)连接CD，交OE于M，

在Rt△ODE中，

∵OD=32，DE=2，

∵OE∥AB，

∴△COE∽△CAB，

∴AB=5，

∵AC是直径，

∵EF∥AB，

∴S△ADF=S梯形ABEFS梯形DBEF

∴△ADF的面积为

【题型】解答题
【结束】
25

【题目】【题目】已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．

（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；

（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；

（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．

【题目】平面直角坐标系 xOy 中，定义：已知图形 W 和直线 l．如果图形 W 上存在一点 Q，使得点 Q 到直线 l 的距离小于或等于 k，则称图形 W 与直线 l“k 关联”，设图形 W：线段 AB，其中点 A（t，0）、点 B（t+2， 0）．

（1）线段AB的长是 ；

（2）当t＝1 时，

①已知直线y＝﹣x﹣1，点A到该直线的距离为 ；

②已知直线y＝﹣x+b，若线段AB与该直线“关联”，求b的取值范围。

【题目】一个质点在第一象限及x轴、y轴上运动在第一秒时，它从原点运动到，然后接着按图中箭头所示方向运动，且每秒移动一个单位长度，那么第2008秒时该质点所在位置的坐标是（ ）

A.B.C.D.

【题目】下列说法正确的是几个（　　）

①2＜2 ＜3；②四边形的内角和与外角和相等；③的立方根为4；④一元二次方程x2﹣6x=10无实数根；⑤若一组数据7，4，x，3，5，6的众数和中位数都是5，则这组数据的平均数也是5．

A. 1 B. 2 C. 3 D. 4

【题目】若将一副三角板按如图所示的方式放置，则下列结论正确的是（　　）

A.∠1＝∠2B.如果∠2＝30°，则有AC∥DE

C.如果∠2＝45°，则有∠4＝∠DD.如果∠2＝50°，则有BC∥AE

【题目】如图，在△ABC中，D是BC边上的中点，∠BDE=∠CDF，请你添加一个条件，使DE=DF成立．你添加的条件是 ．(不再添加辅助线和字母)

【题目】为了迎接旅发大会顺利在织金召开，织金某巡警骑摩托车在南北大道上巡逻，一天他从岗亭出发，晚上停留在A处，规定向北方向为正，当天行驶情况记录如下（单位：千米）：+10，﹣8，+7，﹣15，+6，﹣16，+4，﹣4

（1）A处在岗亭何方？距离岗亭多远？

（2）若摩托车每行驶1千米耗油0.5升，这一天共耗油多少升？

【题目】如图是 2019 年五月的月历，“T”型、“田”型两个阴影图形分别覆盖其中四个方格（可以重叠覆盖），设“T”型阴影覆盖的最小数字为 a，四个数字之和为 S1，“田”型阴影覆盖的最小数字为 b，四个数字之和为 S2.

(1) S1 的值能否为 50？若能，求 a 的值；若不能，说明理由；

(2)S1+ S2 值能否为 35，若能，求 a，b 的值；若不能，说明理由；

(3)若 S1+ S2=43，求 S1－S2 的值为 （直接写结果）.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网