题目内容
直角梯形的一条对角线把梯形分成两个三角形,其中有一个是边长为8的等边三角形,则梯形中位线长是分析:要求梯形的中位线,根据梯形的中位线定理,需要求得梯形的上、下底;结合已知条件,发现根据等边三角形和30°的直角三角形,即可求解.
解答: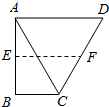 解:∵AD=AC=CD=8,∠CAD=60°
解:∵AD=AC=CD=8,∠CAD=60°
∴∠BAC=90°-∠CAD=90°-60°=30°
在Rt△ABC中,∠BAC=30°
∴BC=
AC=
×8=4
∴梯形中位线长是
(AD+BC)=
(8+4)=6.
故答案为:6.
 解:∵AD=AC=CD=8,∠CAD=60°
解:∵AD=AC=CD=8,∠CAD=60°∴∠BAC=90°-∠CAD=90°-60°=30°
在Rt△ABC中,∠BAC=30°
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
∴梯形中位线长是
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:6.
点评:本题利用梯形的中位线定理以及特殊角的三角函数求解.

练习册系列答案
相关题目
 如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为 ( )
如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为 ( )